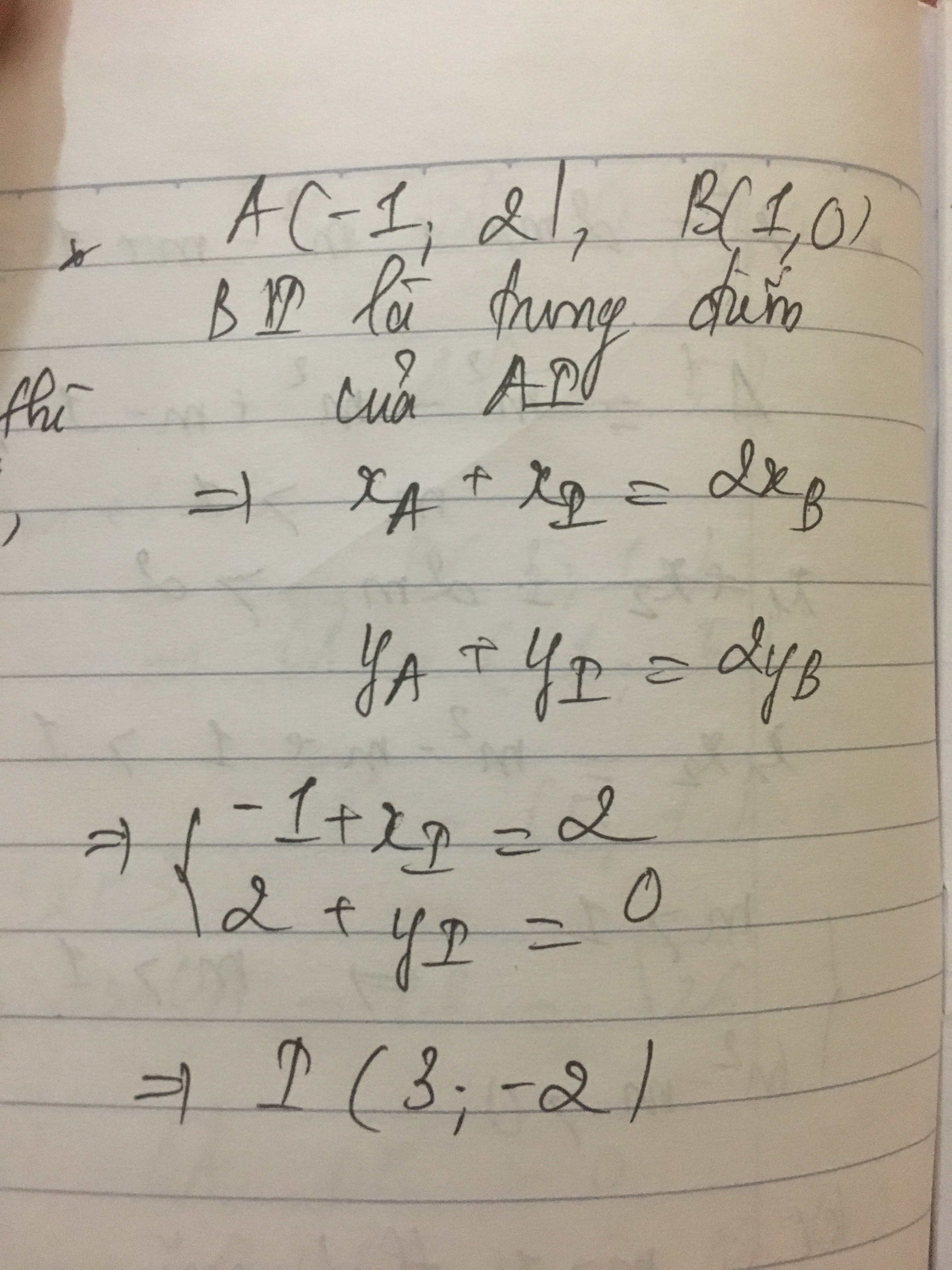Tìm Tọa Độ Điểm D Sao Cho ABCD Là Hình Bình Hành

Trong hình học giải tích, bài toán tìm tọa độ điểm D để tứ giác ABCD trở thành hình bình hành là một dạng toán thường gặp. Bài viết này sẽ trình bày phương pháp giải quyết bài toán này một cách chi tiết và dễ hiểu.

Phương pháp giải tổng quát:

Để tứ giác ABCD là hình bình hành, ta cần chứng minh một trong các điều kiện sau:

1. AB // CD và AD // BC (các cặp cạnh đối song song).
2. AB = CD và AD = BC (các cặp cạnh đối bằng nhau).
3. AB // CD và AB = CD (một cặp cạnh đối song song và bằng nhau).
4. AD // BC và AD = BC (một cặp cạnh đối song song và bằng nhau).
5. Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường.

Trong thực tế, cách tiếp cận phổ biến nhất là sử dụng điều kiện hai đường chéo cắt nhau tại trung điểm. Gọi I là trung điểm của AC. Khi đó, I cũng là trung điểm của BD. Từ đó, ta có thể tìm được tọa độ điểm D.

Ví dụ minh họa:

Cho các điểm A(-2; 0), B(5; -4), C(-5; 1). Hãy tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.

Giải:

Gọi D(x; y) là tọa độ điểm cần tìm.
Để ABCD là hình bình hành thì $overrightarrow{AD} = overrightarrow{BC}$.
Ta có:

• $overrightarrow{AD} = (x + 2; y)$
• $overrightarrow{BC} = (-5 – 5; 1 + 4) = (-10; 5)$

Suy ra, ta có hệ phương trình:

$begin{cases}
x + 2 = -10
y = 5
end{cases}$

Giải hệ phương trình, ta được:

$begin{cases}
x = -12
y = 5
end{cases}$

Vậy tọa độ điểm D là D(-12; 5).

Một cách tiếp cận khác:

Gọi I là trung điểm của AC. Tọa độ của I là:

$I(frac{-2 + (-5)}{2}; frac{0 + 1}{2}) = I(-frac{7}{2}; frac{1}{2})$

Vì I là trung điểm của BD nên:

$begin{cases}
frac{5 + x}{2} = -frac{7}{2}
frac{-4 + y}{2} = frac{1}{2}
end{cases}$

Giải hệ phương trình, ta được:

$begin{cases}
x = -12
y = 5
end{cases}$

Vậy tọa độ điểm D là D(-12; 5).

Lưu ý:

• Khi giải bài toán tìm tọa độ điểm D để ABCD là hình bình hành, cần xác định rõ thứ tự các đỉnh của tứ giác.
• Có thể sử dụng nhiều phương pháp khác nhau để giải bài toán, tùy thuộc vào điều kiện cụ thể của bài toán.
• Kiểm tra lại kết quả bằng cách vẽ hình và kiểm tra xem tứ giác ABCD có thực sự là hình bình hành hay không.

Các dạng bài tập mở rộng:

Ngoài dạng bài tập cơ bản, còn có các dạng bài tập mở rộng liên quan đến hình bình hành, ví dụ:

• Tìm tọa độ điểm D để ABCD là hình bình hành và có diện tích cho trước.
• Tìm tọa độ điểm D để ABCD là hình bình hành và có một góc cho trước.
• Tìm tọa độ điểm D để ABCD là hình bình hành và thỏa mãn một điều kiện nào đó liên quan đến các đường thẳng hoặc đường tròn.

Những dạng bài tập này đòi hỏi người giải phải nắm vững kiến thức về hình học giải tích và có khả năng vận dụng linh hoạt các phương pháp giải toán.

Kết luận:

Bài toán tìm tọa độ điểm D để tứ giác ABCD là hình bình hành là một bài toán cơ bản nhưng quan trọng trong hình học giải tích. Việc nắm vững phương pháp giải và các dạng bài tập mở rộng sẽ giúp học sinh tự tin hơn trong việc giải quyết các bài toán hình học phức tạp hơn. Hy vọng bài viết này đã cung cấp cho bạn đọc những kiến thức hữu ích và giúp bạn đọc hiểu rõ hơn về bài toán này.