Bất phương trình mũ là một phần quan trọng trong chương trình Toán học phổ thông, đặc biệt là trong kỳ thi THPT Quốc gia. Việc nắm vững các phương pháp Tìm Tập Nghiệm của loại bất phương trình này là vô cùng cần thiết để đạt điểm cao. Bài viết này sẽ cung cấp một cái nhìn tổng quan, chi tiết và dễ hiểu về các phương pháp giải bất phương trình mũ, giúp bạn tự tin chinh phục mọi dạng bài.
Để bắt đầu, hãy cùng điểm qua lý thuyết chung về bất phương trình mũ.
1. Bất Phương Trình Mũ Cơ Bản và Tập Nghiệm
Bất phương trình mũ cơ bản có dạng: ax > b (hoặc ax < b, ax ≥ b, ax ≤ b), trong đó a, b là các số đã cho, a > 0 và a ≠ 1.
Việc tìm tập nghiệm của bất phương trình này phụ thuộc vào giá trị của a và b:
- Trường hợp a > 1:
- Nếu b ≤ 0, bất phương trình ax > b đúng với mọi x (tập nghiệm là R).
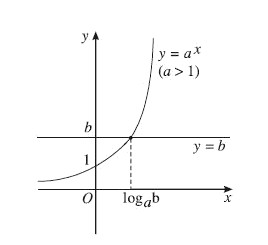
- Nếu b > 0, bất phương trình ax > b tương đương với x > logab.
- Trường hợp 0 < a < 1:
- Nếu b ≤ 0, bất phương trình ax > b đúng với mọi x (tập nghiệm là R).
- Nếu b > 0, bất phương trình ax > b tương đương với x < logab.
![Alt text: Đồ thị hàm số mũ y=a^x với a>1, minh họa tập nghiệm của bất phương trình a^x > b khi b>0 là x > log_a(b). Phân tích đồ thị hàm mũ để xác định nghiệm bất phương trình.]
Hình ảnh trên minh họa cách đồ thị hàm số mũ (với a > 1) được sử dụng để xác định tập nghiệm của bất phương trình ax > b. Dựa vào vị trí tương đối giữa đồ thị và đường thẳng y = b, ta có thể dễ dàng suy ra khoảng giá trị của x thỏa mãn bất phương trình.
![Alt text: Đồ thị hàm số mũ y=a^x với 0<a<1, minh họa tập nghiệm của bất phương trình a^x > b khi b>0 là x < log_a(b). Xác định khoảng nghiệm bất phương trình dựa trên đồ thị hàm số mũ nghịch biến.]
Với trường hợp 0 < a < 1, hình ảnh trên cho thấy đồ thị hàm số mũ nghịch biến và cách nó ảnh hưởng đến việc tìm tập nghiệm của bất phương trình.
2. Các Phương Pháp Tìm Tập Nghiệm Hiệu Quả
Để giải quyết các bất phương trình mũ phức tạp hơn, chúng ta cần áp dụng các phương pháp biến đổi và giải khác. Dưới đây là 3 phương pháp phổ biến nhất:
2.1. Đưa Về Cùng Cơ Số
Đây là phương pháp cơ bản và thường được sử dụng nhất. Ý tưởng chính là biến đổi bất phương trình sao cho cả hai vế đều có cùng cơ số. Sau đó, ta có thể so sánh số mũ dựa trên tính đơn điệu của hàm số mũ.
Ví dụ: Giải bất phương trình 2x+1 < 8.
- Ta có thể viết lại bất phương trình thành 2x+1 < 23.
- Vì cơ số 2 > 1, hàm số mũ đồng biến, nên x + 1 < 3.
- Vậy x < 2. Tập nghiệm là (-∞; 2).
![Alt text: Công thức tổng quát về phương pháp đưa bất phương trình mũ về cùng cơ số. Chuyển đổi cơ số để giải bất phương trình mũ.]
Hình ảnh trên tóm tắt công thức tổng quát cho phương pháp đưa về cùng cơ số, một kỹ thuật quan trọng để tìm tập nghiệm của bất phương trình mũ.
Ngoài ra, ta có thể sử dụng logarit hóa để đưa về cùng cơ số trong một số trường hợp.
![Alt text: Công thức biến đổi logarit hóa để đưa về cùng cơ số. Sử dụng logarit để đơn giản hóa và tìm nghiệm.]
Hình ảnh này minh họa công thức logarit hóa, một công cụ hữu ích khi không thể trực tiếp đưa bất phương trình về cùng cơ số.
Ví dụ minh họa: Tìm tập nghiệm của bất phương trình 4x – 2x+1 – 8 > 0.
![Alt text: Ví dụ 1 bài tập tìm nghiệm của bất phương trình mũ. Phân tích và giải bài tập bằng phương pháp đưa về cùng cơ số.]
![Alt text: Ví dụ 2 bài tập tìm nghiệm của bất phương trình mũ. Ứng dụng phương pháp đưa về cùng cơ số trong bài toán cụ thể.]
2.2. Đặt Ẩn Phụ
Phương pháp này giúp đơn giản hóa bất phương trình bằng cách thay thế một biểu thức phức tạp bằng một ẩn số mới. Sau khi giải bất phương trình với ẩn mới, ta cần thay ngược lại để tìm nghiệm của bất phương trình ban đầu.
Ví dụ: Giải bất phương trình 4x – 3 * 2x + 2 < 0.
- Đặt t = 2x (t > 0). Bất phương trình trở thành t2 – 3t + 2 < 0.
- Giải bất phương trình bậc hai này, ta được 1 < t < 2.
- Thay ngược lại, ta có 1 < 2x < 2.
- Vậy 0 < x < 1. Tập nghiệm là (0; 1).
![Alt text: Ví dụ 3 bài tập tìm nghiệm của bất phương trình mũ bằng phương pháp đặt ẩn phụ. Giải bất phương trình mũ bằng cách đặt ẩn phụ và giải phương trình bậc hai.]
2.3. Đánh Giá và Sử Dụng Tính Đơn Điệu
Trong một số trường hợp, việc biến đổi bất phương trình trở nên khó khăn. Khi đó, ta có thể sử dụng phương pháp đánh giá và dựa vào tính đơn điệu của hàm số để tìm tập nghiệm.
Ví dụ: Giải bất phương trình 3x + x > 4.
- Nhận thấy x = 1 là một nghiệm của bất phương trình (31 + 1 = 4).
- Xét hàm số f(x) = 3x + x. Hàm số này đồng biến trên R (tổng của hai hàm đồng biến).
- Do đó, nếu x > 1 thì f(x) > f(1) = 4, và nếu x < 1 thì f(x) < f(1) = 4.
- Vậy tập nghiệm của bất phương trình là (1; +∞).
![Alt text: Ví dụ 4 bài tập tìm tập nghiệm của bất phương trình mũ bằng phương pháp đánh giá tính đơn điệu. Sử dụng tính đơn điệu của hàm số mũ để tìm khoảng nghiệm.]
3. Lưu Ý Quan Trọng Khi Tìm Tập Nghiệm
- Luôn kiểm tra điều kiện của ẩn (nếu có) sau khi đặt ẩn phụ.
- Cẩn thận với dấu của bất phương trình khi nhân hoặc chia cả hai vế cho một số âm.
- Khi sử dụng tính đơn điệu, cần chứng minh hàm số đồng biến hoặc nghịch biến trên khoảng xét.
- Biết cách vẽ và đọc đồ thị hàm số mũ.
4. Bài Tập Luyện Tập
Để củng cố kiến thức, hãy tự giải các bài tập sau:
- 2x > 16
- (1/3)x < 9
- 5x+1 + 5-x > 6
- 9x – 4 * 3x + 3 < 0
Việc luyện tập thường xuyên là chìa khóa để nắm vững các phương pháp tìm tập nghiệm của bất phương trình mũ. Chúc các bạn thành công!