Tam thức bậc hai đóng vai trò quan trọng trong chương trình toán học phổ thông và các kỳ thi. Một trong những dạng toán thường gặp là “Tìm m để f(x) ≥ 0”, đòi hỏi sự hiểu biết sâu sắc về dấu của tam thức bậc hai. Bài viết này sẽ cung cấp kiến thức toàn diện và phương pháp giải quyết hiệu quả cho dạng toán này, giúp bạn tự tin chinh phục mọi bài tập.
1. Ôn lại kiến thức cơ bản về tam thức bậc hai
Tam thức bậc hai là biểu thức có dạng:
f(x) = ax² + bx + c
Trong đó:
- x là biến số.
- a, b, c là các hệ số, với a ≠ 0.
Nghiệm của tam thức bậc hai là nghiệm của phương trình ax² + bx + c = 0.
Hình ảnh minh họa định nghĩa và các hệ số trong tam thức bậc hai.
2. Dấu của tam thức bậc hai: Điều kiện để f(x) ≥ 0
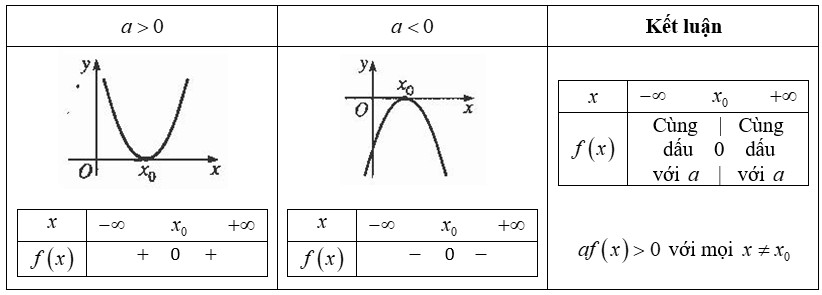
2.1. Định lý về dấu
Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0) và biệt thức Δ = b² – 4ac.
- Δ < 0: f(x) cùng dấu với a với mọi x ∈ R. Nếu a > 0 thì f(x) > 0 ∀ x ∈ R; nếu a < 0 thì f(x) < 0 ∀ x ∈ R.
- Δ = 0: f(x) có nghiệm kép x = -b/2a. f(x) cùng dấu với a với mọi x ≠ -b/2a. Nếu a > 0 thì f(x) ≥ 0 ∀ x ∈ R; nếu a < 0 thì f(x) ≤ 0 ∀ x ∈ R.
- Δ > 0: f(x) có hai nghiệm phân biệt x₁ và x₂ (x₁ < x₂).
- f(x) cùng dấu với a khi x < x₁ hoặc x > x₂.
- f(x) trái dấu với a khi x₁ < x < x₂.
2.2. Khi nào thì f(x) ≥ 0 với mọi x?
Đây là trọng tâm của bài toán “Tìm m để f(x) ≥ 0”. Để f(x) ≥ 0 với mọi x ∈ R, ta cần xét hai điều kiện:
- a > 0: Đảm bảo parabol hướng lên trên.
- Δ ≤ 0: Đảm bảo parabol không cắt hoặc chỉ tiếp xúc với trục hoành.
2.3. Minh họa hình học
Hình ảnh minh họa các trường hợp đồ thị tam thức bậc hai tương ứng với các giá trị khác nhau của delta.
3. Các bước giải bài toán “Tìm m để f(x) ≥ 0”
- Xác định hệ số a, b, c: Xác định rõ các hệ số của tam thức bậc hai f(x) = ax² + bx + c, đặc biệt chú ý đến hệ số a (có chứa tham số m hay không).
- Lập điều kiện a > 0: Giải bất phương trình a > 0 để tìm khoảng giá trị của m.
- Tính biệt thức Δ: Tính Δ = b² – 4ac. Biệt thức này thường chứa tham số m.
- Lập điều kiện Δ ≤ 0: Giải bất phương trình Δ ≤ 0 để tìm khoảng giá trị của m.
- Kết hợp điều kiện: Tìm giao của các khoảng giá trị của m tìm được ở bước 2 và bước 4. Đây chính là tập hợp các giá trị của m để f(x) ≥ 0 với mọi x.
- Xét trường hợp đặc biệt: Nếu a chứa tham số m và có thể bằng 0, cần xét riêng trường hợp a = 0 để đảm bảo không bỏ sót nghiệm. Khi a = 0, f(x) trở thành hàm bậc nhất và điều kiện f(x) ≥ 0 có thể dễ dàng xác định.
4. Ví dụ minh họa
Ví dụ: Tìm m để f(x) = x² – 2(m+1)x + m² + 3 ≥ 0 với mọi x ∈ R.
Giải:
- Xác định hệ số: a = 1, b = -2(m+1), c = m² + 3.
- Điều kiện a > 0: a = 1 > 0 (luôn đúng, không phụ thuộc vào m).
- Tính biệt thức: Δ = [-2(m+1)]² – 4(1)(m² + 3) = 4(m² + 2m + 1) – 4m² – 12 = 8m – 8.
- Điều kiện Δ ≤ 0: 8m – 8 ≤ 0 ⇔ m ≤ 1.
- Kết hợp điều kiện: Vì a > 0 luôn đúng, ta chỉ cần điều kiện m ≤ 1.
Vậy, m ≤ 1 thì f(x) ≥ 0 với mọi x ∈ R.
5. Lưu ý quan trọng
- Kiểm tra lại kết quả: Sau khi tìm được khoảng giá trị của m, hãy thử thay một vài giá trị cụ thể vào f(x) để kiểm tra xem điều kiện f(x) ≥ 0 có thực sự được thỏa mãn hay không.
- Sử dụng đồ thị: Vẽ phác họa đồ thị của f(x) để kiểm tra trực quan kết quả.
- Nắm vững các trường hợp đặc biệt: Chú ý các trường hợp a = 0 hoặc khi phương trình có nghiệm kép.
6. Bài tập tự luyện
- Tìm m để f(x) = -x² + mx – 1 ≤ 0 với mọi x ∈ R.
- Tìm m để f(x) = (m-1)x² + 2(m-1)x + 3 > 0 với mọi x ∈ R.
- Tìm m để f(x) = mx² – 4x + m + 3 ≥ 0 với mọi x ∈ R.
7. Tổng kết
Bài toán “Tìm m để f(x) ≥ 0” là một dạng toán quan trọng liên quan đến tam thức bậc hai. Việc nắm vững lý thuyết về dấu của tam thức bậc hai, kết hợp với các bước giải bài tập logic và cẩn thận, sẽ giúp bạn giải quyết dạng toán này một cách hiệu quả. Chúc các bạn thành công!
Bảng xét dấu minh họa cho việc xác định khoảng giá trị của x để f(x) dương, âm hoặc bằng 0.