Tìm GTLN, GTNN của Hàm Số Trên Khoảng, Đoạn: Phương Pháp và Bài Tập Chi Tiết

Bài viết này sẽ đi sâu vào phương pháp tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số trên một khoảng hoặc một đoạn, kèm theo các ví dụ minh họa chi tiết và bài tập áp dụng. Đây là một chủ đề quan trọng trong chương trình Toán học phổ thông và thường xuyên xuất hiện trong các kỳ thi.

I. Tìm GTLN, GTNN của Hàm Số Trên Khoảng, Nửa Khoảng

1. Phương Pháp Chung

Để tìm GTLN và GTNN của hàm số $f(x)$ trên một khoảng $D$, ta thường sử dụng bảng biến thiên (BBT). Bảng biến thiên giúp ta hình dung được sự biến thiên của hàm số và xác định các điểm cực trị, từ đó suy ra GTLN và GTNN.

Cần lưu ý rằng, khi đề bài chỉ yêu cầu tìm GTLN, GTNN của hàm số $f(x)$ mà không chỉ rõ khoảng xét, ta hiểu là tìm trên tập xác định của hàm số đó.

2. Ví dụ Minh Họa

Ví dụ 1: Tìm GTLN và GTNN của hàm số $y = frac{3x – 2}{x – 1}$ trên khoảng $(1; +infty)$.

Lời giải:

• Bước 1: Tính đạo hàm: $y’ = frac{3(-1) – (-2).1}{(x – 1)^2} = frac{-1}{(x – 1)^2} < 0, forall x in (1; +infty)$.

• Bước 2: Lập bảng biến thiên:

  x	1	$+infty$
  y’		–
  y	$-infty$	3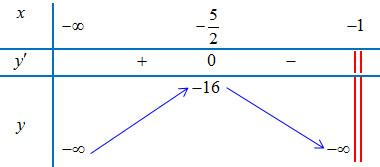

  

  

• Bước 3: Kết luận:

  • Không tồn tại GTLN trên $(1; +infty)$.
  • Không tồn tại GTNN trên $(1; +infty)$.

Ví dụ 2: Tìm GTLN và GTNN của hàm số $y = frac{4x – 3}{x + 2}$ trên nửa khoảng $(-2; 7]$.

Lời giải:

• Bước 1: Tính đạo hàm: $y’ = frac{4.2 – (-3).1}{(x + 2)^2} = frac{11}{(x + 2)^2} > 0, forall x in (-2; 7]$.

• Bước 2: Lập bảng biến thiên:

![Bang bien thien ham so y=(4x-3)/(x+2) tren nua khoang (-2;7]](http://donghochetac.store/wp-content/uploads/2025/04/bang-bien-thien-ham-so-y4x-3×2-tren-nua-khoang-27.jpg){width=343 height=144}

Alt text: Bảng biến thiên của hàm số y=(4x-3)/(x+2) trên nửa khoảng (-2;7], thể hiện sự đồng biến của hàm số.

• Bước 3: Kết luận:

  • GTLN: $max_{(-2; 7]} y = y(7) = frac{25}{9}$.
  • Không tồn tại GTNN trên $(-2; 7]$.

Ví dụ 3: Tìm GTLN và GTNN của hàm số $y = frac{x^2 – 2x + 16}{x – 2}$ trên khoảng $(2; +infty)$.

Lời giải:

• Bước 1: Tính đạo hàm:

  $y’ = frac{(2x – 2)(x – 2) – (x^2 – 2x + 16)}{(x – 2)^2} = frac{x^2 – 4x – 12}{(x – 2)^2}$.

• Bước 2: Giải phương trình $y’ = 0$:

  $x^2 – 4x – 12 = 0 Leftrightarrow begin{cases} x = 6 quad (nhận) x = -2 quad (loại) end{cases}$.

• Bước 3: Lập bảng biến thiên:

  x	2	6	$+infty$
  y’		0	+
  y	$+infty$	10	$+infty$

• Bước 4: Kết luận:

  • GTNN: $min_{(2; +infty)} y = y(6) = 10$.
  • Không tồn tại GTLN trên $(2; +infty)$.

Ví dụ 4: Tìm GTLN và GTNN của hàm số $y = frac{4x^2 + 4x + 9}{x + 1}$ trên khoảng $(-infty; -1)$.

Lời giải:

• Bước 1: Tính đạo hàm:

  $y’ = frac{(8x + 4)(x + 1) – (4x^2 + 4x + 9)}{(x + 1)^2} = frac{4x^2 + 8x – 5}{(x + 1)^2}$.

• Bước 2: Giải phương trình $y’ = 0$:

  $4x^2 + 8x – 5 = 0 Leftrightarrow begin{cases} x = frac{1}{2} quad (loại) x = -frac{5}{2} quad (nhận) end{cases}$.

• Bước 3: Lập bảng biến thiên:

Alt text: Bảng biến thiên hàm số y=(4x^2+4x+9)/(x+1) trên khoảng âm vô cùng đến -1, minh họa điểm cực đại của hàm số.

• Bước 4: Kết luận:

  • GTLN: $max_{(-infty; -1)} y = y(-frac{5}{2}) = -16$.
  • Không tồn tại GTNN trên $(-infty; -1)$.

Ví dụ 5: Tìm GTLN và GTNN của hàm số $y = frac{2x^2 – 3}{x^2 + 2}$.

Lời giải:

• Bước 1: Tập xác định: $D = mathbb{R}$.

• Bước 2: Tính đạo hàm:

  $y’ = frac{4x(x^2 + 2) – (2x^2 – 3)2x}{(x^2 + 2)^2} = frac{14x}{(x^2 + 2)^2}$.

• Bước 3: Giải phương trình $y’ = 0$:

  $14x = 0 Leftrightarrow x = 0$.

• Bước 4: Lập bảng biến thiên:

  x	$-infty$	0	$+infty$
  y’	–	0	+
  y	2	-3/2	2

• Bước 5: Kết luận:

  • GTNN: $min_{mathbb{R}} y = y(0) = -frac{3}{2}$.
  • Không tồn tại GTLN trên $mathbb{R}$.

Ví dụ 6: Tìm GTLN và GTNN của hàm số $y = sqrt{x^2 – 25}$.

Lời giải:

• Bước 1: Tập xác định: $D = (-infty; -5] cup [5; +infty)$.

• Bước 2: Tính đạo hàm:

  $y’ = frac{2x}{2sqrt{x^2 – 25}} = frac{x}{sqrt{x^2 – 25}}$.

• Bước 3: Giải phương trình $y’ = 0$:

  $x = 0$ (loại).

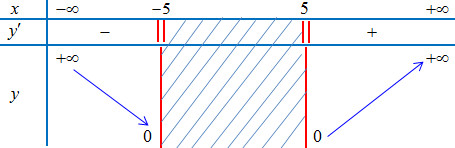
• Bước 4: Lập bảng biến thiên:

Alt text: Bảng biến thiên của hàm số y = căn bậc hai của (x^2 – 25), thể hiện điểm cực tiểu tại x = -5 và x = 5.

• Bước 5: Kết luận:

  • GTNN: $min_{D} y = y(-5) = y(5) = 0$.
  • Không tồn tại GTLN trên $D$.

II. Tìm GTLN, GTNN của Hàm Số Trên Một Đoạn

1. Phương Pháp

Để tìm GTLN và GTNN của hàm số $f(x)$ trên đoạn $[a; b]$, ta thực hiện các bước sau:

1. Tìm các điểm $x_1, x_2, …, x_n in (a; b)$ mà tại đó $f'(x) = 0$ hoặc $f'(x)$ không tồn tại.
2. Tính các giá trị $f(x_1), f(x_2), …, f(x_n), f(a), f(b)$.
3. So sánh các giá trị trên, giá trị lớn nhất là GTLN và giá trị nhỏ nhất là GTNN của hàm số trên đoạn $[a; b]$.

2. Ví dụ Minh Họa

Ví dụ 7: Tìm GTLN và GTNN của hàm số $y = x^3 – 3x^2 + 5$ trên đoạn $[1; 4]$.

Lời giải:

• Bước 1: Tính đạo hàm: $y’ = 3x^2 – 6x$.
• Bước 2: Giải phương trình $y’ = 0$: $3x^2 – 6x = 0 Leftrightarrow begin{cases} x = 2 x = 0 quad (loại) end{cases}$.
• Bước 3: Tính các giá trị: $y(1) = 3$, $y(4) = 21$, $y(2) = 1$.
• Bước 4: Kết luận:
  • GTLN: $max_{[1; 4]} y = y(4) = 21$.
  • GTNN: $min_{[1; 4]} y = y(2) = 1$.

Ví dụ 8: Tìm GTLN và GTNN của hàm số $y = -x^4 + 8x^2 + 4$ trên đoạn $[-sqrt{5}; 2]$.

Lời giải:

• Bước 1: Tính đạo hàm: $y’ = -4x^3 + 16x$.
• Bước 2: Giải phương trình $y’ = 0$: $-4x^3 + 16x = 0 Leftrightarrow begin{cases} x = 2 x = 0 x = -2 end{cases}$.
• Bước 3: Tính các giá trị: $y(-sqrt{5}) = 19$, $y(2) = 20$, $y(0) = 4$, $y(-2) = 20$.
• Bước 4: Kết luận:
  • GTLN: $max_{[-sqrt{5}; 2]} y = y(-2) = y(2) = 20$.
  • GTNN: $min_{[-sqrt{5}; 2]} y = y(0) = 4$.

Ví dụ 9: Tìm GTLN và GTNN của hàm số $y = frac{-3x + 5}{x – 7}$ trên đoạn $[-3; 0]$.

Lời giải:

• Bước 1: Tính đạo hàm: $y’ = frac{16}{(x – 7)^2} > 0, forall x in [-3; 0]$.
• Bước 2: Tính các giá trị: $y(-3) = -frac{7}{5}$, $y(0) = -frac{5}{7}$.
• Bước 3: Kết luận:
  • GTLN: $max_{[-3; 0]} y = y(0) = -frac{5}{7}$.
  • GTNN: $min_{[-3; 0]} y = y(-3) = -frac{7}{5}$.

Ví dụ 10: Tìm GTLN và GTNN của hàm số $y = sqrt{27 – 3x^2}$.

Lời giải:

• Bước 1: Tập xác định: $D = [-3; 3]$.
• Bước 2: Tính đạo hàm: $y’ = frac{-6x}{2sqrt{27 – 3x^2}} = frac{-3x}{sqrt{27 – 3x^2}}$.
• Bước 3: Giải phương trình $y’ = 0$: $-3x = 0 Leftrightarrow x = 0$.
• Bước 4: Tính các giá trị: $y(-3) = 0$, $y(3) = 0$, $y(0) = 3sqrt{3}$.
• Bước 5: Kết luận:
  • GTLN: $max_{[-3; 3]} y = y(0) = 3sqrt{3}$.
  • GTNN: $min_{[-3; 3]} y = y(-3) = y(3) = 0$.

Ví dụ 11: Tìm GTLN và GTNN của hàm số $y = sqrt{-x^2 + 8x – 7}$.

Lời giải:

• Bước 1: Tập xác định: $D = [1; 7]$.
• Bước 2: Tính đạo hàm: $y’ = frac{-2x + 8}{2sqrt{-x^2 + 8x – 7}} = frac{-x + 4}{sqrt{-x^2 + 8x – 7}}$.
• Bước 3: Giải phương trình $y’ = 0$: $-x + 4 = 0 Leftrightarrow x = 4$.
• Bước 4: Tính các giá trị: $y(1) = 0$, $y(7) = 0$, $y(4) = 3$.
• Bước 5: Kết luận:
  • GTLN: $max_{[1; 7]} y = y(4) = 3$.
  • GTNN: $min_{[1; 7]} y = y(1) = y(7) = 0$.

Ví dụ 12 (Đề thi Tốt nghiệp THPT năm 2024): Giá trị lớn nhất của hàm số $f(x) = -6x^3 + 27x^2 – 16x + 1$ trên đoạn $[1; 5]$ bằng bao nhiêu?

Lời giải:

• Bước 1: Tính đạo hàm: $f'(x) = -18x^2 + 54x – 16$.
• Bước 2: Giải phương trình $f'(x) = 0$: $-18x^2 + 54x – 16 = 0 Leftrightarrow begin{cases} x = frac{8}{3} quad (nhận) x = frac{1}{3} quad (loại) end{cases}$.
• Bước 3: Tính các giá trị: $f(1) = 6$, $f(5) = -154$, $f(frac{8}{3}) = frac{329}{9}$.
• Bước 4: Kết luận: $max_{[1; 5]} f(x) = f(frac{8}{3}) = frac{329}{9}$.

Chọn B.

Kết luận

Việc tìm GTLN và GTNN của hàm số trên một khoảng hoặc một đoạn là một kỹ năng quan trọng trong giải toán. Bằng cách nắm vững phương pháp và luyện tập thường xuyên, bạn sẽ có thể giải quyết các bài toán liên quan một cách dễ dàng và chính xác.