Để hiểu rõ về đồ thị hàm số và cách xác định một điểm có thuộc đồ thị hay không, chúng ta sẽ đi sâu vào định nghĩa, phương pháp kiểm tra và các ví dụ minh họa chi tiết.
1. Định Nghĩa Đồ Thị Hàm Số
Cho hàm số (y = f(x)) xác định trên tập hợp D. Đồ thị của hàm số này là tập hợp tất cả các điểm (M(x; f(x))) trên mặt phẳng tọa độ, với mọi giá trị x thuộc D. Ta ký hiệu đồ thị này là ((C) = { M(x;f(x)) | x in D }). Nói cách khác, đồ thị hàm số là hình ảnh trực quan biểu diễn mối quan hệ giữa biến số x và giá trị tương ứng của hàm số y.
2. Kiểm Tra Điểm Thuộc Đồ Thị Hàm Số
Để xác định một điểm (M(x_M; y_M)) có thuộc đồ thị hàm số (y = f(x)) hay không, ta cần kiểm tra hai điều kiện sau:
- Điều kiện 1: (x_M in D) (xM phải thuộc tập xác định của hàm số).
- Điều kiện 2: (y_M = f(x_M)) (yM phải bằng giá trị của hàm số tại xM).
Nếu cả hai điều kiện trên đồng thời thỏa mãn, thì điểm (M(x_M; y_M)) thuộc đồ thị hàm số (y = f(x)). Ngược lại, nếu ít nhất một trong hai điều kiện không thỏa mãn, thì điểm đó không thuộc đồ thị hàm số.
Ví dụ: Xét hàm số (y = x + 1) và điểm (A(2; 3)).
- Ta thấy (x_A = 2) thuộc tập xác định của hàm số (tập số thực).
- Tính (f(x_A) = f(2) = 2 + 1 = 3). Vì (y_A = 3 = f(2)), nên điểm A thuộc đồ thị hàm số (y = x + 1).
3. Ví Dụ Minh Họa
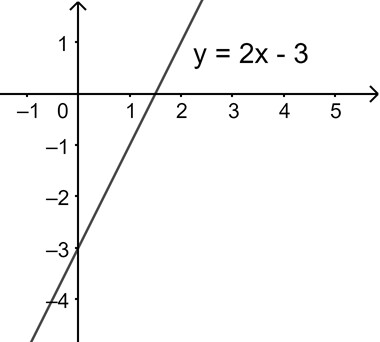
Xét đồ thị hàm số (y = 2x – 3).
Đồ thị hàm số (y = 2x – 3) là một đường thẳng. Để vẽ đường thẳng này, ta chỉ cần xác định hai điểm thuộc đồ thị. Ví dụ:
- Khi (x = 0), ta có (y = 2(0) – 3 = -3). Vậy điểm (0; -3) thuộc đồ thị.
- Khi (x = 1.5), ta có (y = 2(1.5) – 3 = 0). Vậy điểm (1.5; 0) thuộc đồ thị.
Nối hai điểm này lại, ta được đồ thị hàm số (y = 2x – 3).
Xét đồ thị hàm số (y = x^2 – 4).
Từ đồ thị, ta thấy:
- Các điểm (2; 0), (-2; 0), (1; -3), (0; -4) thuộc đồ thị hàm số.
- Các điểm (2; 2), (-2; 3), (1; 2), (0; 3) không thuộc đồ thị hàm số.
4. Bài Tập Vận Dụng
Bài 1: Cho hàm số (y = x^2 + 1). Điểm nào sau đây thuộc đồ thị hàm số?
A. (1; 1)
B. (0; 0)
C. (1; 2)
D. (-1; 0)
Hướng dẫn giải:
- Kiểm tra điểm (1; 1): (f(1) = 1^2 + 1 = 2 ne 1). Loại A.
- Kiểm tra điểm (0; 0): (f(0) = 0^2 + 1 = 1 ne 0). Loại B.
- Kiểm tra điểm (1; 2): (f(1) = 1^2 + 1 = 2). Chọn C.
- Kiểm tra điểm (-1; 0): (f(-1) = (-1)^2 + 1 = 2 ne 0). Loại D.
Vậy đáp án đúng là C. (1; 2).
Bài 2: Cho hàm số (y = frac{1}{x}). Điểm nào sau đây không thuộc đồ thị hàm số?
A. (1; 1)
B. (2; frac{1}{2})
C. (-1; -1)
D. (0; 0)
Hướng dẫn giải:
Hàm số (y = frac{1}{x}) không xác định khi (x = 0). Do đó, điểm (0; 0) không thuộc đồ thị hàm số.
Kết luận:
Việc nắm vững định nghĩa và phương pháp kiểm tra điểm thuộc đồ thị hàm số là rất quan trọng trong việc giải các bài toán liên quan đến hàm số và đồ thị. Hy vọng qua bài viết này, bạn đã có cái nhìn tổng quan và chi tiết hơn về chủ đề này. Hãy luyện tập thêm các bài tập để củng cố kiến thức và kỹ năng của mình.