Trong giải tích, tiệm cận là một khái niệm quan trọng, đặc biệt khi nghiên cứu đồ thị hàm số. Một câu hỏi thường gặp là “Tiệm Cận Ngang Là X Hay Y?”. Bài viết này sẽ giải đáp thắc mắc đó một cách chi tiết, đồng thời cung cấp các phương pháp xác định tiệm cận ngang hiệu quả.
Tiệm Cận Ngang Là Gì?
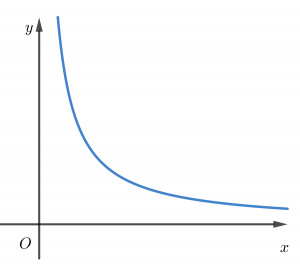
Tiệm cận ngang là một đường thẳng mà đồ thị hàm số tiến gần đến khi x tiến đến vô cùng (âm vô cùng hoặc dương vô cùng). Quan trọng cần nhớ, tiệm cận ngang là một đường thẳng có dạng y = b, trong đó b là một hằng số. Điều này có nghĩa là giá trị y của hàm số dần tiến đến b khi x càng lớn hoặc càng nhỏ.
Đồ thị minh họa tiệm cận ngang, cho thấy giá trị y của hàm số dần tiến đến giá trị b (đường tiệm cận ngang) khi x tiến ra vô cực.
Cách Tìm Tiệm Cận Ngang Của Đồ Thị Hàm Số
Để tìm tiệm cận ngang của đồ thị hàm số y = f(x), ta thực hiện các bước sau:
- Tìm tập xác định (TXĐ) của hàm số: Xác định các giá trị của x mà hàm số có nghĩa.
- Tính giới hạn của hàm số khi x tiến đến vô cực:
- Tính $lim_{x to +infty} f(x)$. Nếu giới hạn này bằng b (một số thực), thì y = b là một tiệm cận ngang.
- Tính $lim_{x to -infty} f(x)$. Nếu giới hạn này bằng c (một số thực), thì y = c là một tiệm cận ngang. Lưu ý rằng b và c có thể khác nhau, vì vậy một hàm số có thể có tối đa hai tiệm cận ngang.
Ví dụ: Cho hàm số $y = frac{x+1}{x^2+1}$. Tìm tiệm cận ngang của đồ thị hàm số.
- Tập xác định: D = R (tất cả các số thực)
- Tính giới hạn:
- $lim_{x to +infty} frac{x+1}{x^2+1} = 0$
- $lim_{x to -infty} frac{x+1}{x^2+1} = 0$
Vậy, đồ thị hàm số có một tiệm cận ngang là y = 0.
Công Thức Tính Tiệm Cận Ngang
Tiệm Cận Ngang Của Hàm Phân Thức Hữu Tỉ
Cho hàm số $y = frac{P(x)}{Q(x)}$, trong đó P(x) và Q(x) là các đa thức. Ta có các trường hợp sau:
- Bậc của P(x) < Bậc của Q(x): Tiệm cận ngang là y = 0.
- Bậc của P(x) = Bậc của Q(x): Tiệm cận ngang là $y = frac{a}{b}$, trong đó a là hệ số của số hạng bậc cao nhất của P(x) và b là hệ số của số hạng bậc cao nhất của Q(x).
- Bậc của P(x) > Bậc của Q(x): Không có tiệm cận ngang.
Bảng tóm tắt cách xác định tiệm cận ngang cho hàm phân thức hữu tỉ dựa vào so sánh bậc của đa thức ở tử và mẫu số.
Tiệm Cận Ngang Của Hàm Phân Thức Vô Tỉ
Đối với hàm phân thức vô tỉ, việc xác định tiệm cận ngang phức tạp hơn và thường cần phải tính giới hạn một cách trực tiếp. Tuy nhiên, một số dạng thường gặp có thể áp dụng công thức hoặc biến đổi để đưa về dạng quen thuộc.
Bảng tóm tắt công thức xác định tiệm cận ngang cho hàm phân thức vô tỉ. Cần chú ý đến tập xác định và các phép biến đổi để đơn giản biểu thức trước khi tính giới hạn.
Cách Tính Đường Tiệm Cận Ngang Bằng Máy Tính
Máy tính cầm tay có thể hỗ trợ tính giới hạn gần đúng để tìm tiệm cận ngang.
- Nhập hàm số vào máy tính.
- Sử dụng chức năng CALC (hoặc tương đương) để tính giá trị của hàm số tại x rất lớn và x rất nhỏ.
- Để tính $lim_{x to +infty} f(x)$, nhập $x = 10^9$ (hoặc một số lớn tương tự).
- Để tính $lim_{x to -infty} f(x)$, nhập $x = -10^9$ (hoặc một số nhỏ tương tự).
- Kết quả hiển thị trên máy tính sẽ xấp xỉ giá trị của giới hạn. Nếu kết quả là một số thực b, thì y = b là tiệm cận ngang.
Hình ảnh minh họa các bước sử dụng máy tính Casio để tính giới hạn của hàm số khi x tiến đến vô cực, từ đó xác định tiệm cận ngang.
Xác Định Tiệm Cận Ngang Qua Bảng Biến Thiên
Bảng biến thiên (BBT) cung cấp thông tin về sự biến thiên của hàm số, bao gồm cả giới hạn tại vô cực và các điểm đặc biệt. Để xác định tiệm cận ngang từ BBT:
- Xác định tập xác định của hàm số từ BBT.
- Quan sát giá trị của y khi x tiến đến $+infty$ và $-infty$. Nếu y tiến đến một giá trị hữu hạn b, thì y = b là tiệm cận ngang.
Bài Tập Vận Dụng
Bài 1: Tìm tiệm cận ngang của đồ thị hàm số $y = frac{x + sqrt{4x^2 – 3}}{2x + 3}$.
Giải:
- $lim{x to -infty} y = lim{x to -infty} frac{x – sqrt{4x^2 – 3}}{2x + 3} = frac{1 – 2}{2} = -frac{1}{2}$
- $lim{x to +infty} y = lim{x to +infty} frac{x + sqrt{4x^2 – 3}}{2x + 3} = frac{1 + 2}{2} = frac{3}{2}$
Vậy, y = 3/2 và y = -1/2 là các tiệm cận ngang của đồ thị hàm số.
Bài 2: Cho hàm số $y = sqrt{m^2 + 2x} – x$. Tìm m để đồ thị hàm số có tiệm cận ngang.
Bài toán tìm giá trị của tham số m để hàm số có tiệm cận ngang. Cần phân tích giới hạn của hàm số khi x tiến đến vô cực và biện luận theo m.
Lời giải: Để hàm số có tiệm cận ngang, giới hạn của y khi x tiến đến vô cực phải tồn tại và hữu hạn.
$lim_{x to +infty} (sqrt{m^2 + 2x} – x)$
Để giải quyết giới hạn này, ta nhân và chia cho biểu thức liên hợp:
$lim{x to +infty} frac{(sqrt{m^2 + 2x} – x)(sqrt{m^2 + 2x} + x)}{sqrt{m^2 + 2x} + x} = lim{x to +infty} frac{m^2 + 2x – x^2}{sqrt{m^2 + 2x} + x} = lim_{x to +infty} frac{-x^2 + 2x + m^2}{sqrt{m^2 + 2x} + x}$
Để giới hạn này tồn tại và hữu hạn, bậc của tử phải nhỏ hơn hoặc bằng bậc của mẫu. Tuy nhiên, bậc của tử là 2, còn bậc của mẫu là 1. Do đó, giới hạn này không tồn tại. Vậy không có giá trị m nào thỏa mãn để hàm số có tiệm cận ngang.
Kết Luận
Tiệm cận ngang là một đường thẳng có dạng y = b, cho biết giá trị mà hàm số dần tiến đến khi x tiến đến vô cực. Việc xác định tiệm cận ngang có thể được thực hiện bằng cách tính giới hạn, sử dụng công thức cho hàm phân thức, hoặc quan sát bảng biến thiên. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về tiệm cận ngang và cách xác định chúng.