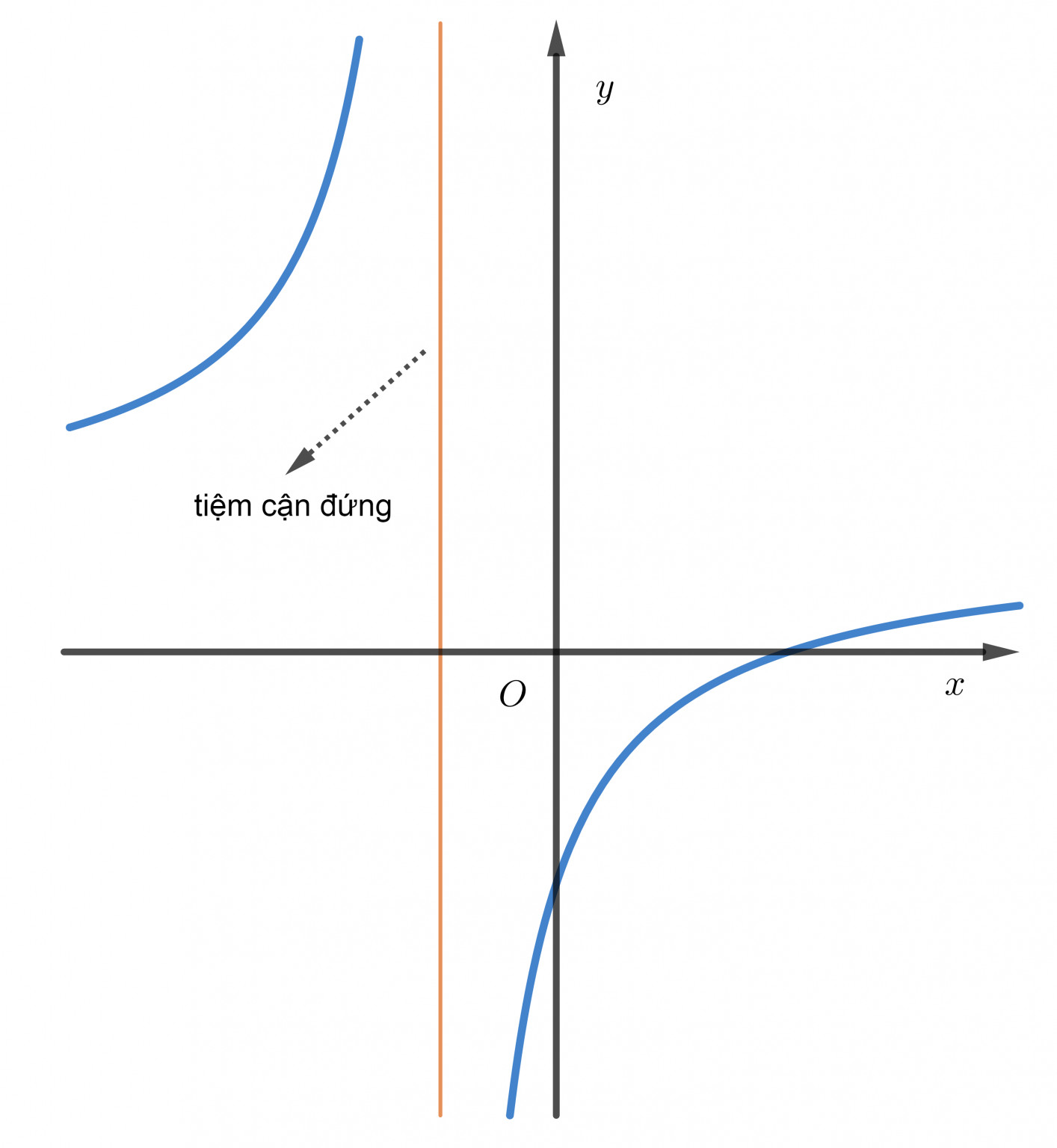
Tiệm cận đứng là một khái niệm quan trọng trong giải tích, đặc biệt khi xét đồ thị hàm số. Việc xác định chính xác tiệm cận đứng giúp chúng ta hiểu rõ hơn về hình dáng và tính chất của đồ thị. Vậy tiệm cận đứng là y hay x? Bài viết này sẽ giúp bạn trả lời câu hỏi đó và cung cấp các phương pháp tìm tiệm cận đứng hiệu quả nhất.
1. Định Nghĩa Tiệm Cận Đứng
Tiệm cận đứng của đồ thị hàm số y = f(x) là đường thẳng mà đồ thị hàm số tiến gần đến vô cùng khi x tiến đến một giá trị cụ thể. Về mặt toán học, đường thẳng x = x₀ được gọi là tiệm cận đứng của đồ thị hàm số y = f(x) nếu thỏa mãn ít nhất một trong các điều kiện sau:
 Định nghĩa tiệm cận đứng qua giới hạn một bên.
Định nghĩa tiệm cận đứng qua giới hạn một bên.
Trong đó:
- lim ₓ→ₓ₀⁺ f(x) = ±∞ : Giới hạn của f(x) khi x tiến đến x₀ từ bên phải bằng vô cùng.
- lim ₓ→ₓ₀⁻ f(x) = ±∞ : Giới hạn của f(x) khi x tiến đến x₀ từ bên trái bằng vô cùng.
Vậy, tiệm cận đứng là đường thẳng có dạng x = x₀, tức là một đường thẳng song song với trục tung (trục Oy).
2. Các Bước Tìm Tiệm Cận Đứng
Để tìm tiệm cận đứng của đồ thị hàm số, ta thực hiện theo các bước sau:
- Xác định tập xác định D của hàm số: Tìm tất cả các giá trị của x mà hàm số có nghĩa.
- Tìm các điểm mà hàm số không xác định: Đây thường là các điểm mà mẫu số của phân thức bằng 0 hoặc các điểm mà hàm số không liên tục.
- Tính giới hạn một bên tại các điểm không xác định: Tính lim ₓ→ₓ₀⁺ f(x) và lim ₓ→ₓ₀⁻ f(x) tại các điểm không xác định x₀.
- Kết luận: Nếu ít nhất một trong hai giới hạn trên bằng ±∞, thì x = x₀ là tiệm cận đứng của đồ thị hàm số.
Ví dụ: Tìm tiệm cận đứng của hàm số y = (x – 2) / (x² – 4)
-
Tập xác định: D = R {-2, 2}
-
Hàm số không xác định tại x = -2 và x = 2
-
Tính giới hạn:
- lim ₓ→₂ f(x) = lim ₓ→₂ (x – 2) / (x² – 4) = lim ₓ→₂ 1 / (x + 2) = 1/4 (x = 2 không là tiệm cận đứng)
-
Kết luận: x = -2 là tiệm cận đứng của đồ thị hàm số.
3. Công Thức Nhanh Cho Hàm Phân Thức Bậc Nhất
Đối với hàm số phân thức bậc nhất có dạng y = (ax + b) / (cx + d) (với ad – bc ≠ 0 và c ≠ 0), ta có thể áp dụng công thức sau để tìm nhanh tiệm cận đứng:
- Tiệm cận đứng: x = -d/c
Ví dụ: Tìm tiệm cận đứng của hàm số y = (x – 2) / (x + 3)
Áp dụng công thức, ta có tiệm cận đứng là x = -3.
4. Tìm Tiệm Cận Đứng Bằng Máy Tính
Máy tính cầm tay là một công cụ hữu ích để hỗ trợ tìm tiệm cận đứng, đặc biệt với các hàm số phức tạp. Các bước thực hiện như sau:
- Tìm nghiệm của mẫu số: Sử dụng chức năng SOLVE hoặc EQN (giải phương trình) để tìm nghiệm của phương trình mẫu số = 0.
- Kiểm tra nghiệm trên tử số: Sử dụng chức năng CALC (tính giá trị biểu thức) để kiểm tra xem các nghiệm vừa tìm được có đồng thời là nghiệm của tử số hay không.
- Kết luận: Các nghiệm của mẫu số mà không phải là nghiệm của tử số là các giá trị x₀ mà x = x₀ là tiệm cận đứng.
Ví dụ: Tìm tiệm cận đứng của hàm số y = (2x – 1 – √(x² + x + 3)) / (x² – 5x + 6)
- Giải phương trình x² – 5x + 6 = 0, ta được x = 2 và x = 3.
- Kiểm tra tử số:
- Với x = 2, tử số bằng 0.
- Với x = 3, tử số khác 0.
- Kết luận: x = 3 là tiệm cận đứng của đồ thị hàm số.
5. Nhận Biết Tiệm Cận Đứng Qua Bảng Biến Thiên
Bảng biến thiên cũng là một công cụ hữu ích để xác định tiệm cận đứng. Dựa vào bảng biến thiên, ta có thể nhận biết tiệm cận đứng thông qua các dấu hiệu sau:
- Tìm tập xác định: Xác định các giá trị x mà hàm số không xác định.
- Quan sát: Tìm các điểm mà tại đó f(x) tiến đến ±∞.
- Kết luận: Các giá trị x mà hàm số không xác định và tại đó f(x) tiến đến ±∞ là các tiệm cận đứng.
6. Bài Tập Vận Dụng
6.1. Dạng 1: Xác Định Tiệm Cận Đứng Dựa Trên Định Nghĩa
Cho hàm số y = (2x – 3) / (x – 1). Tìm tiệm cận đứng.
- Tập xác định: D = R {1}
- lim ₓ→₁⁺ (2x – 3) / (x – 1) = -∞
- lim ₓ→₁⁻ (2x – 3) / (x – 1) = +∞
- Kết luận: x = 1 là tiệm cận đứng.
6.2. Dạng 2: Tiệm Cận Đứng Của Hàm Phân Thức
Cho hàm số y = (1 – 3x) / (x + 2). Tìm tiệm cận đứng.
- Áp dụng công thức nhanh: x = -2
- Kết luận: x = -2 là tiệm cận đứng.
6.3. Dạng 3: Tìm Tham Số m Để Hàm Số Có Tiệm Cận Đứng
Cho hàm số y = (3x + 1) / (m – 2x). Tìm giá trị của m để đường thẳng x = 1 là tiệm cận đứng.
- Để x = 1 là tiệm cận đứng, mẫu số phải bằng 0 tại x = 1, tức là m – 2(1) = 0 => m = 2.
- Kiểm tra lại: Với m = 2, hàm số trở thành y = (3x + 1) / (2 – 2x). Rõ ràng x = 1 là tiệm cận đứng.
- Kết luận: m = 2.
Hy vọng qua bài viết này, bạn đã nắm vững kiến thức về tiệm cận đứng, hiểu rõ tiệm cận đứng là x hay y, và biết cách áp dụng các phương pháp để giải nhanh các bài tập liên quan. Chúc các bạn thành công trong học tập!
