Tỉ Lệ Nghịch là một khái niệm toán học quan trọng, xuất hiện thường xuyên trong cả lý thuyết và ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn toàn diện về tỉ lệ nghịch, từ định nghĩa cơ bản đến các dạng bài tập thường gặp và cách giải quyết chúng.
Định Nghĩa và Tính Chất Của Tỉ Lệ Nghịch
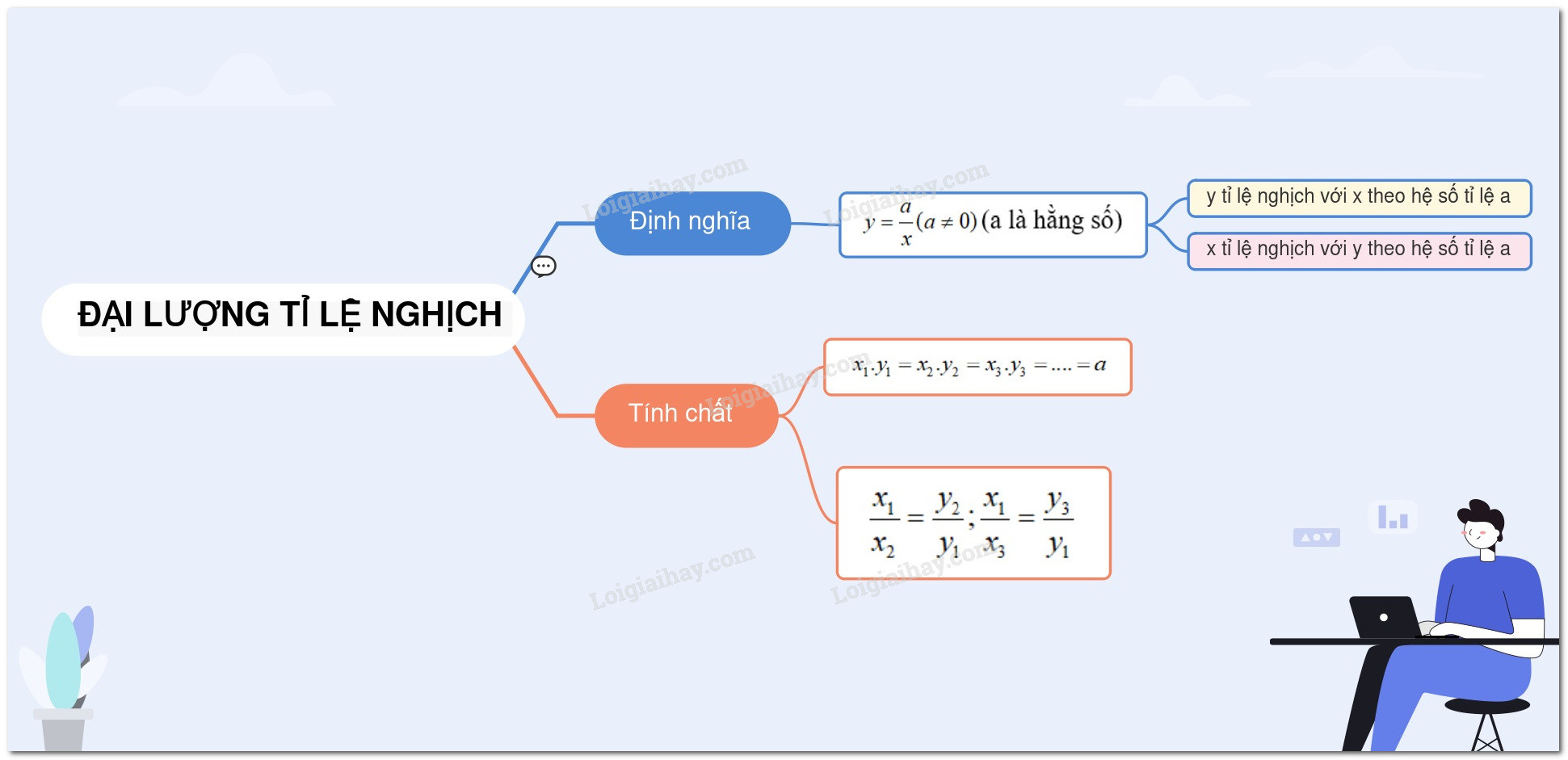
Định Nghĩa Tỉ Lệ Nghịch
Hai đại lượng được gọi là tỉ lệ nghịch với nhau nếu tích của chúng là một hằng số khác không. Nói cách khác, nếu đại lượng y liên hệ với đại lượng x theo công thức y = a/x hoặc xy = a (với a là hằng số khác 0), thì y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
Ví dụ: Nếu y = 5/x, thì y tỉ lệ nghịch với x theo hệ số tỉ lệ là 5. Điều này có nghĩa là khi x tăng lên, y sẽ giảm xuống và ngược lại, sao cho tích của chúng luôn bằng 5.
Đồ thị minh họa mối quan hệ tỉ lệ nghịch giữa x và y, cho thấy khi x tăng, y giảm và ngược lại, với đường cong hyperbol đặc trưng.
Tính Chất Quan Trọng Của Tỉ Lệ Nghịch
- Tích không đổi: Tích của hai giá trị tương ứng của hai đại lượng tỉ lệ nghịch luôn là một hằng số. Nếu
ytỉ lệ nghịch vớixtheo hệ số tỉ lệa, thìx1*y1 = x2*y2 = x3*y3 = ... = a. - Tỉ số nghịch đảo: Tỉ số của hai giá trị bất kỳ của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia. Nếu
ytỉ lệ nghịch vớix, thìx1/x2 = y2/y1; x1/x3 = y3/y1;...
Các Dạng Toán Về Tỉ Lệ Nghịch Thường Gặp
1. Bảng Giá Trị Tương Ứng
Phương pháp:
- Tìm hệ số tỉ lệ: Xác định hệ số tỉ lệ
abằng cách nhân một cặp giá trịxvàytương ứng. - Tính giá trị còn thiếu: Sử dụng công thức
y = a/xhoặcx = a/yđể tìm các giá trịxhoặcycòn thiếu trong bảng.
2. Xác Định Tương Quan Tỉ Lệ Nghịch
Phương pháp:
Kiểm tra xem tích của các cặp giá trị tương ứng của hai đại lượng có bằng nhau hay không. Nếu tất cả các tích đều bằng nhau, hai đại lượng đó tỉ lệ nghịch. Ngược lại, nếu có ít nhất một cặp giá trị có tích khác, thì hai đại lượng không tỉ lệ nghịch.
3. Bài Toán Ứng Dụng Thực Tế
Phương pháp:
- Xác định đại lượng: Xác định rõ các đại lượng được đề cập trong bài toán.
- Xác định mối quan hệ: Xác định xem giữa các đại lượng có mối quan hệ tỉ lệ nghịch hay không.
- Áp dụng tính chất: Áp dụng tính chất của tỉ lệ nghịch để lập tỉ lệ thức và giải bài toán.
Ví dụ: Số công nhân và thời gian hoàn thành công việc (nếu năng suất mỗi công nhân như nhau) là hai đại lượng tỉ lệ nghịch.
4. Chia Tỉ Lệ Nghịch
Phương pháp:
Chia một số M thành các phần x, y, z tỉ lệ nghịch với các số a, b, c. Ta có:
ax = by = cz hay x/(1/a) = y/(1/b) = z/(1/c).
Để chia số M thành các phần tỉ lệ nghịch với các số a, b, c, ta thực chất chia số M thành các phần tỉ lệ thuận với các số 1/a, 1/b, 1/c. Sau đó áp dụng quy tắc chia tỉ lệ thuận.
Bài Tập Vận Dụng
Ví dụ 1: Một xe tải đi từ A đến B với vận tốc 40 km/h mất 3 giờ. Hỏi nếu xe tải đó đi với vận tốc 60 km/h thì mất bao lâu?
Giải:
Gọi thời gian xe tải đi với vận tốc 60 km/h là t (giờ). Vì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch, ta có:
40 * 3 = 60 * t
t = (40 * 3) / 60 = 2
Vậy, nếu xe tải đi với vận tốc 60 km/h thì mất 2 giờ.
Ví dụ 2: Ba người cùng góp vốn kinh doanh. Người thứ nhất góp 2 triệu đồng, người thứ hai góp 3 triệu đồng, người thứ ba góp 5 triệu đồng. Tổng lợi nhuận thu được là 20 triệu đồng. Chia lợi nhuận cho mỗi người tỉ lệ nghịch với số vốn đã góp. Hỏi mỗi người nhận được bao nhiêu tiền lãi?
Giải:
Gọi số tiền lãi của ba người lần lượt là x, y, z (triệu đồng). Theo đề bài, ta có:
2x = 3y = 5z và x + y + z = 20.
Suy ra x/(1/2) = y/(1/3) = z/(1/5).
Áp dụng tính chất của dãy tỉ số bằng nhau:
x/(1/2) = y/(1/3) = z/(1/5) = (x + y + z) / (1/2 + 1/3 + 1/5) = 20 / (31/30) = 600/31.
Từ đó, ta tính được:
x = (600/31) * (1/2) = 300/31 ≈ 9.68 triệu đồng.
y = (600/31) * (1/3) = 200/31 ≈ 6.45 triệu đồng.
z = (600/31) * (1/5) = 120/31 ≈ 3.87 triệu đồng.
Kết luận:
Hiểu rõ về tỉ lệ nghịch giúp chúng ta giải quyết nhiều bài toán thực tế một cách dễ dàng và chính xác. Hãy luyện tập thường xuyên để nắm vững kiến thức này và áp dụng nó vào các tình huống khác nhau trong cuộc sống.
