Trong hình học giải tích, việc tính thể tích khối tròn xoay tạo thành khi quay một hình phẳng quanh một trục là một bài toán quan trọng và thú vị. Bài viết này sẽ cung cấp kiến thức toàn diện về cách tính “Thể Tích Khối Tròn Xoay Thu được Khi Quay Hình Phẳng Giới Hạn Bởi 2 đường”, cùng các ví dụ minh họa từ cơ bản đến nâng cao.
1. Khái Niệm Khối Tròn Xoay
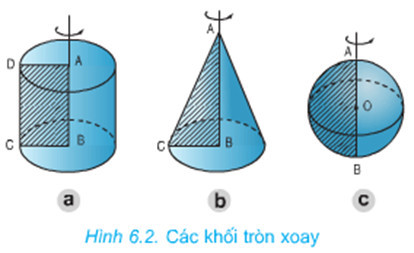
Khối tròn xoay là hình được tạo thành khi quay một hình phẳng quanh một trục cố định. Các hình tròn xoay thường gặp là hình nón, hình trụ, hình cầu. Việc tính thể tích của chúng có ứng dụng rộng rãi trong nhiều lĩnh vực.
Minh họa trực quan về các khối tròn xoay thường gặp như hình nón, hình trụ và hình cầu, giúp người đọc dễ hình dung và nắm bắt khái niệm.
2. Công Thức Tính Thể Tích Khối Tròn Xoay Quanh Trục Ox
Xét hình phẳng giới hạn bởi các đường:
y = f(x)y = g(x)x = ax = b
Với f(x) ≥ g(x) trên đoạn [a, b].
Thể tích khối tròn xoay tạo thành khi quay hình phẳng này quanh trục Ox được tính theo công thức:
V = π ∫[a, b] (f(x)² - g(x)²) dx
Công thức này dựa trên nguyên lý “phương pháp đĩa” (disk method) hoặc “phương pháp vòng” (washer method) trong tích phân.
3. Công Thức Tính Thể Tích Khối Tròn Xoay Quanh Trục Oy
Tương tự, xét hình phẳng giới hạn bởi các đường:
x = f(y)x = g(y)y = cy = d
Với f(y) ≥ g(y) trên đoạn [c, d].
Thể tích khối tròn xoay tạo thành khi quay hình phẳng này quanh trục Oy được tính theo công thức:
V = π ∫[c, d] (f(y)² - g(y)²) dy
4. Ví Dụ Minh Họa
Ví dụ 1: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = √x, y = 0 và x = 4 quanh trục Ox.
Áp dụng công thức:
Công thức tích phân quen thuộc để tính thể tích khối tròn xoay, được trình bày rõ ràng để người đọc dễ dàng tham khảo và áp dụng.
Ta có:
V = π ∫[0, 4] (√x)² dx = π ∫[0, 4] x dx = π [x²/2] |[0, 4] = 8π
Ví dụ 2: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = x² và y = x quanh trục Ox.
Đầu tiên, tìm giao điểm của hai đường: x² = x => x = 0 hoặc x = 1.
V = π ∫[0, 1] (x² - (x²)²) dx = π ∫[0, 1] (x² - x⁴) dx = π [(x³/3) - (x⁵/5)] |[0, 1] = 2π/15
Ví dụ 3: Cho hình phẳng (H) giới hạn bởi đồ thị hàm số , trục Ox và đường thẳng x=1. Tính thể tích khối tròn xoay thu được khi xoay (H) quanh trục Ox.
Hình ảnh trực quan về hình phẳng (H), giúp người đọc hình dung rõ hơn về miền tích phân và các đường biên.
Ví dụ 4: Thể tích V của khối tròn xoay được hình thành bằng cách quay quanh hình phẳng được giới hạn bằng các đường , y=0, x=4 và trục Ox. Đường thẳng x=a (0 tại M.
Hình ảnh minh họa rõ ràng về quá trình tạo thành khối tròn xoay, giúp người đọc hiểu rõ hơn về mối quan hệ giữa hình phẳng và thể tích.
5. Lưu Ý Khi Giải Bài Tập
- Xác định chính xác các đường giới hạn hình phẳng.
- Tìm giao điểm của các đường để xác định cận tích phân.
- Xác định hàm nào lớn hơn hàm nào trên đoạn tích phân (để đảm bảo
f(x) ≥ g(x)). - Áp dụng đúng công thức tính thể tích.
- Kiểm tra lại kết quả.
6. Ứng Dụng Thực Tế
Việc tính “thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi 2 đường” có nhiều ứng dụng trong thực tế, ví dụ:
- Kỹ thuật: Tính toán thể tích các chi tiết máy có hình dạng tròn xoay.
- Xây dựng: Tính toán thể tích các cấu trúc có hình dạng tròn xoay như mái vòm, bể chứa.
- Y học: Mô phỏng và tính toán thể tích các bộ phận cơ thể.
Hy vọng bài viết này đã cung cấp cho bạn kiến thức đầy đủ và chi tiết về cách tính “thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi 2 đường”. Chúc các bạn học tốt!