Trong chương trình hình học không gian, khái niệm về khối tròn xoay và thể tích của chúng đóng vai trò quan trọng. Bài viết này sẽ tập trung vào cách tính Thể Tích Khối Tròn Xoay Quanh Trục Ox, cung cấp công thức, ví dụ minh họa và bài tập áp dụng giúp bạn nắm vững kiến thức này.
1. Khối Tròn Xoay Là Gì?
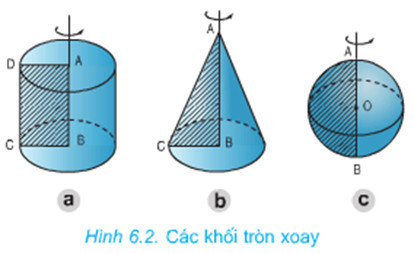
Khối tròn xoay là hình được tạo thành khi quay một hình phẳng quanh một trục cố định. Các hình tròn xoay thường gặp bao gồm hình nón, hình trụ và hình cầu. Việc tính thể tích của các khối này có nhiều ứng dụng trong thực tế.
Hình ảnh minh họa các hình khối tròn xoay cơ bản, giúp người đọc hình dung trực quan về đối tượng nghiên cứu và thể tích của chúng.
2. Công Thức Tính Thể Tích Khối Tròn Xoay Quanh Trục Ox
Để tính thể tích khối tròn xoay khi quay quanh trục Ox, ta xét các trường hợp sau:
Trường hợp 1: Hình phẳng giới hạn bởi đường cong y = f(x), trục hoành (y = 0), và hai đường thẳng x = a, x = b.
Trong trường hợp này, công thức tính thể tích V của khối tròn xoay là:
Trường hợp 2: Hình phẳng giới hạn bởi hai đường cong y = f(x), y = g(x) (với g(x) ≤ f(x) ∀ x ∈ [a, b]), và hai đường thẳng x = a, x = b.
Khi đó, công thức tính thể tích V của khối tròn xoay là:
Công thức này dựa trên việc tính hiệu thể tích giữa hai khối tròn xoay tạo bởi f(x) và g(x).
3. Ví Dụ Minh Họa
Để hiểu rõ hơn về cách áp dụng công thức, chúng ta sẽ xét một số ví dụ cụ thể:
Ví dụ 1: Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường thẳng y = 1 – x², trục Ox, và hai đường thẳng x = 0, x = 1 quanh trục Ox.
Giải:
Áp dụng công thức:
Ta có:
Hình ảnh minh họa cách áp dụng công thức vào bài toán cụ thể, giúp người học nắm bắt phương pháp giải và các bước tính toán.
Ví dụ 2: Cho hình phẳng giới hạn bởi đồ thị hàm số , trục Ox và đường thẳng x=1. Hãy tính thể tích khối tròn xoay thu được đó khi xoay quanh hình (H) và xoay quanh trục Ox.
Hình ảnh minh họa hình phẳng và cách xác định cận tích phân, giúp người học hình dung bài toán và áp dụng công thức một cách chính xác.
4. Bài Tập Ứng Dụng
Để củng cố kiến thức, bạn có thể thử sức với các bài tập sau:
- Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường cong y = √x, trục Ox và đường thẳng x = 4 quanh trục Ox.
- Tính thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đường cong y = x², đường thẳng y = x quanh trục Ox.
5. Lưu Ý Khi Tính Thể Tích Khối Tròn Xoay
- Xác định chính xác hàm số f(x) và g(x) (nếu có).
- Xác định đúng cận tích phân a và b.
- Tính toán cẩn thận các bước tích phân.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Việc nắm vững công thức và luyện tập thường xuyên sẽ giúp bạn tự tin giải quyết các bài toán liên quan đến thể tích khối tròn xoay quanh trục Ox. Chúc bạn thành công!