Trong chương trình hình học không gian, Thể Tích Hình Tròn Xoay là một khái niệm quan trọng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về thể tích hình tròn xoay, bao gồm định nghĩa, công thức tính toán, các trường hợp đặc biệt và bài tập minh họa.
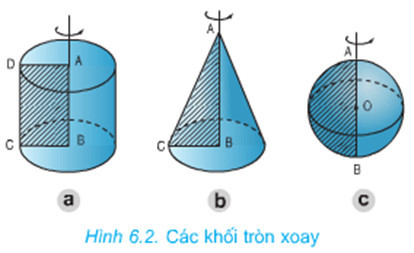
Hình tròn xoay được tạo thành khi một hình phẳng quay quanh một trục cố định. Các hình tròn xoay phổ biến bao gồm hình nón, hình trụ và hình cầu.
Minh họa thể tích hình tròn xoay: Hình nón, hình trụ và hình cầu được tạo ra bằng cách quay các hình phẳng tương ứng quanh một trục.
Công Thức Tính Thể Tích Hình Tròn Xoay
Để tính thể tích hình tròn xoay, ta xét hai trường hợp chính: quay quanh trục Ox và quay quanh trục Oy.
1. Thể Tích Hình Tròn Xoay Khi Quay Quanh Trục Ox
Giả sử ta có một hàm số y = f(x) liên tục trên đoạn [a, b]. Khi quay đồ thị hàm số này quanh trục Ox, ta thu được một hình tròn xoay.
Công thức tính thể tích V của hình tròn xoay này là:
Trong trường hợp hình phẳng giới hạn bởi hai đường cong y = f(x) và y = g(x) (với f(x) ≥ g(x) trên [a, b]), trục Ox và hai đường thẳng x = a, x = b, thể tích hình tròn xoay tạo thành là:
2. Thể Tích Hình Tròn Xoay Khi Quay Quanh Trục Oy
Tương tự, ta xét hàm số x = g(y) liên tục trên đoạn [c, d]. Khi quay đồ thị hàm số này quanh trục Oy, ta thu được một hình tròn xoay.
Công thức tính thể tích V của hình tròn xoay này là:
Nếu hình phẳng giới hạn bởi hai đường cong x = f(y) và x = g(y) (với f(y) ≥ g(y) trên [c, d]), trục Oy và hai đường thẳng y = c, y = d, thể tích hình tròn xoay tạo thành là:
Bài Tập Về Thể Tích Hình Tròn Xoay
Ví dụ 1: Tính thể tích hình tròn xoay tạo thành khi quay đường cong y = 1 – x² quanh trục Ox, giới hạn bởi y = 0, x = 0 và x = 2.
Giải:
Áp dụng công thức thể tích hình tròn xoay khi quay quanh trục Ox:
Ta có:
Ví dụ 1 về thể tích hình tròn xoay: Tính thể tích khi quay đường cong y=1-x^2 quanh trục Ox.
Ví dụ 2: Cho hình phẳng giới hạn bởi y = 2/x, trục Oy, y = 1 và y = 4. Tính thể tích hình tròn xoay khi quay hình này quanh trục Oy.
Ví dụ 2 về thể tích hình tròn xoay: Tính thể tích khi quay đường cong y=2/x quanh trục Oy.
Ví dụ 3: Tính thể tích hình tròn xoay tạo thành khi quay hình phẳng giới hạn bởi y = √x , y = -x + 2, và y = 0 quanh trục Oy.
Ví dụ 3 về thể tích hình tròn xoay: Tính thể tích khi quay hình phẳng giới hạn bởi y = √x , y = -x + 2, và y = 0 quanh trục Oy.
Ví dụ 4: Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số , trục Ox và đường thẳng x = 1. Tính thể tích hình tròn xoay thu được khi xoay (H) quanh trục Ox.
Ví dụ 4 về thể tích hình tròn xoay: Tính thể tích khi quay hình phẳng (H) quanh trục Ox với hàm số y=√[x/(4-x^2)].
Ví dụ 5: Thể tích V của khối tròn xoay được tạo thành bằng cách quay quanh hình phẳng được giới hạn bằng các đường , y = 0, x = 4 và trục Ox. Đường thẳng x = a (0 tại M.
Ví dụ 5 về thể tích hình tròn xoay: Tính thể tích khối tròn xoay khi quay quanh hình phẳng giới hạn bởi y=√x, y=0, x=4 và trục Ox.
Gọi V1 là thể tích hình tròn xoay được tạo thành khi quay tam giác MOH quanh trục Ox. Biết rằng V = 2V1. Tính a?
Ví dụ 6 về thể tích hình tròn xoay: Tính giá trị a khi biết V=2V1, V1 là thể tích khi quay tam giác MOH quanh trục Ox.
Hy vọng qua bài viết này, bạn đã nắm vững kiến thức về thể tích hình tròn xoay, các công thức tính và ứng dụng của chúng trong giải toán. Chúc bạn học tốt!