Elip là một hình học quan trọng, và việc tính thể tích của khối tròn xoay tạo bởi elip là một bài toán thú vị trong giải tích. Bài viết này sẽ cung cấp kiến thức toàn diện về Thể Tích Hình Elip, bao gồm công thức tính, ứng dụng thực tế và các ví dụ minh họa.
Công thức tính thể tích hình elip
Xét elip có phương trình chính tắc:
x²/a² + y²/b² = 1
Khi elip này quay quanh trục Ox, ta được một khối tròn xoay. Thể tích V của khối tròn xoay này được tính bằng công thức tích phân:
V = π ∫[-a, a] y² dx
Thay y² = b²(1 – x²/a²) vào công thức trên, ta có:
V = π ∫[-a, a] b²(1 – x²/a²) dx
V = πb² ∫[-a, a] (1 – x²/a²) dx
V = πb² [x – x³/(3a²)] |[-a, a]
V = πb² [(a – a³/3a²) – (-a + a³/3a²)]
V = πb² [2a – 2a/3]
V = πb² [4a/3]
V = (4/3)πab²
Vậy, thể tích của khối tròn xoay tạo bởi elip khi quay quanh trục Ox là:
V = (4/3)πab²
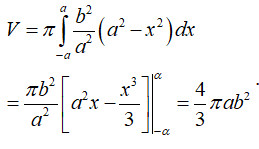Hình elip quay quanh trục Ox tạo thành khối tròn xoay
Công thức trên thể hiện rõ mối quan hệ giữa thể tích khối tròn xoay elip với bán trục lớn a và bán trục bé b của elip.
Ví dụ minh họa
Tính thể tích khối tròn xoay tạo thành khi elip x²/9 + y²/4 = 1 quay quanh trục Ox.
Áp dụng công thức V = (4/3)πab² với a = 3 và b = 2, ta có:
V = (4/3)π(3)(2²) = (4/3)π(3)(4) = 16π
Vậy thể tích của khối tròn xoay là 16π đơn vị thể tích.
Ứng dụng thực tế
Việc tính thể tích hình elip không chỉ là một bài toán lý thuyết mà còn có nhiều ứng dụng trong thực tế, ví dụ như:
- Thiết kế các loại bồn chứa: Các bồn chứa có hình dạng elip hoặc gần elip có thể được tính toán thể tích chính xác để đảm bảo khả năng chứa và tối ưu hóa không gian.
- Tính toán trong xây dựng: Trong một số công trình kiến trúc, việc tính toán thể tích các cấu trúc elip là cần thiết để đảm bảo tính toán vật liệu và tải trọng chính xác.
- Ứng dụng trong y học: Trong y học, việc ước tính thể tích của các cơ quan có hình dạng gần elip (ví dụ như một số bộ phận của tim) có thể giúp các bác sĩ đưa ra chẩn đoán chính xác hơn.
- Trong thiên văn học: Tính toán thể tích của các thiên thạch hoặc các thiên thể có hình dạng gần elip.
Bài tập tự luyện
- Tính thể tích khối tròn xoay tạo bởi elip x²/16 + y²/9 = 1 khi quay quanh trục Ox.
- Một bồn chứa có hình dạng elip với bán trục lớn a = 5m và bán trục bé b = 3m. Tính thể tích của bồn chứa đó.
- Tìm thể tích của vật thể tròn xoay tạo thành khi cho elip có phương trình x²/4 + y²/1 = 1 quay quanh trục Ox.
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về thể tích hình elip, công thức tính, ứng dụng và các ví dụ minh họa. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán liên quan và áp dụng vào thực tế một cách hiệu quả.