Thể tích khối tứ diện đều cạnh a là một kiến thức quan trọng trong hình học không gian. Bài viết này sẽ cung cấp công thức, cách tính, và ứng dụng của nó một cách chi tiết và dễ hiểu nhất.
Công thức tính thể tích khối tứ diện đều cạnh a
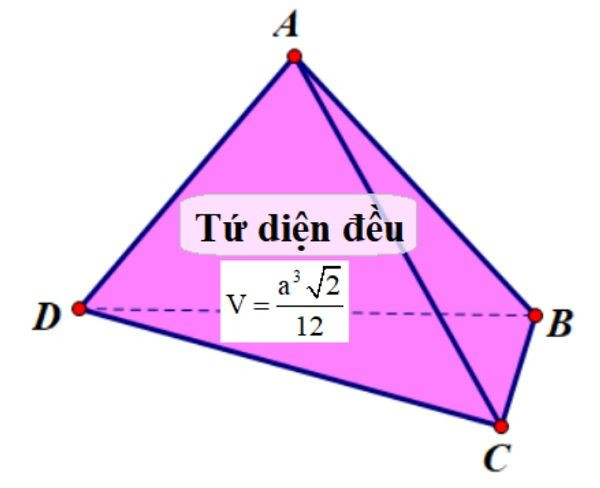
Công thức tính thể tích khối tứ diện đều cạnh a là:
V = (a³√2) / 12
Trong đó:
- V là thể tích của khối tứ diện đều.
- a là độ dài cạnh của khối tứ diện đều.
- √2 là căn bậc hai của 2 (xấp xỉ 1.414).
Hình ảnh trực quan về khối tứ diện đều và công thức tính thể tích giúp người đọc dễ dàng hình dung và ghi nhớ kiến thức.
Các bước tính thể tích khối tứ diện đều cạnh a
Để tính thể tích khối tứ diện đều cạnh a, ta thực hiện các bước sau:
-
Xác định độ dài cạnh a: Đo hoặc xác định độ dài cạnh của khối tứ diện đều.
-
Tính a³ (a mũ 3): Lấy độ dài cạnh a nhân với chính nó hai lần (a a a).
-
Nhân a³ với √2: Lấy kết quả ở bước 2 nhân với căn bậc hai của 2 (√2 ≈ 1.414).
-
Chia kết quả cho 12: Lấy kết quả ở bước 3 chia cho 12.
Kết quả cuối cùng chính là thể tích của khối tứ diện đều.
Ví dụ minh họa cách tính thể tích khối tứ diện đều
Giả sử, ta có một khối tứ diện đều có cạnh a = 6 cm. Hãy tính thể tích của khối tứ diện này.
-
Xác định a: a = 6 cm
-
Tính a³: a³ = 6 6 6 = 216 cm³
-
Nhân a³ với √2: 216 √2 ≈ 216 1.414 ≈ 305.424 cm³
-
Chia kết quả cho 12: 305.424 / 12 ≈ 25.452 cm³
Vậy, thể tích của khối tứ diện đều cạnh 6 cm là khoảng 25.452 cm³.
Hình ảnh minh họa giúp người đọc hiểu rõ hơn về cách áp dụng công thức vào bài toán cụ thể.
Ứng dụng của công thức tính thể tích khối tứ diện đều
Công thức tính thể tích khối tứ diện đều có nhiều ứng dụng trong thực tế và trong các bài toán hình học không gian, ví dụ như:
- Tính thể tích các vật thể có hình dạng gần đúng khối tứ diện đều: Trong kiến trúc và xây dựng, có thể cần tính thể tích gần đúng của các vật thể có hình dạng phức tạp.
- Giải các bài toán hình học: Công thức này là cơ sở để giải nhiều bài toán liên quan đến khối tứ diện đều, chẳng hạn như tìm mối liên hệ giữa thể tích và các yếu tố khác của khối tứ diện.
- Ứng dụng trong thiết kế và mô phỏng: Trong lĩnh vực thiết kế đồ họa và mô phỏng 3D, việc tính toán thể tích là cần thiết để tạo ra các mô hình chính xác và thực tế.
Hình ảnh thể hiện ứng dụng thực tế của việc tính thể tích khối tứ diện đều trong kiến trúc, giúp người đọc thấy được tính ứng dụng của kiến thức.
Lưu ý quan trọng khi tính thể tích khối tứ diện đều
- Đơn vị đo: Đảm bảo rằng tất cả các đơn vị đo đều thống nhất trước khi thực hiện tính toán. Nếu cạnh a được đo bằng cm, thì thể tích sẽ được tính bằng cm³.
- Tính chính xác: Sử dụng máy tính hoặc công cụ tính toán để đảm bảo tính chính xác của các phép tính, đặc biệt là khi làm việc với căn bậc hai của 2.
- Kiểm tra lại kết quả: Luôn kiểm tra lại kết quả để tránh sai sót trong quá trình tính toán.
Hy vọng bài viết này đã cung cấp cho bạn đầy đủ thông tin về thể tích của khối tứ diện đều cạnh a, cùng với công thức, cách tính và các ứng dụng thực tế của nó.