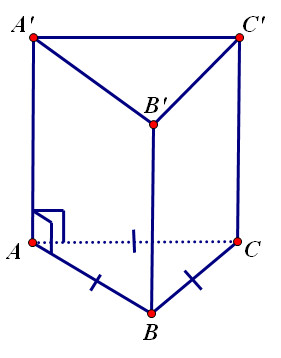
Khối lăng trụ tam giác đều là một hình học quan trọng, xuất hiện nhiều trong các bài toán và ứng dụng thực tế. Hiểu rõ về định nghĩa, tính chất và công thức tính Thể Tích Của Khối Lăng Trụ Tam Giác đều là nền tảng vững chắc để chinh phục các bài toán hình học không gian.
1. Lăng Trụ Tam Giác Đều Là Gì?
Lăng trụ tam giác đều là hình lăng trụ có hai đáy là hai tam giác đều bằng nhau và các mặt bên là hình chữ nhật. Đây là một trường hợp đặc biệt của lăng trụ tam giác, mang những đặc điểm riêng biệt.
2. Tính Chất Của Lăng Trụ Tam Giác Đều
Nắm vững các tính chất giúp dễ dàng nhận diện và áp dụng công thức tính thể tích của khối lăng trụ tam giác đều một cách chính xác:
- Hai đáy là hai tam giác đều bằng nhau.
- Các cạnh đáy bằng nhau.
- Các mặt bên là các hình chữ nhật bằng nhau.
- Các mặt bên vuông góc với hai mặt đáy.
3. Công Thức Tính Thể Tích Khối Lăng Trụ Tam Giác Đều
Công thức tính thể tích của khối lăng trụ tam giác đều vô cùng quan trọng và thường được sử dụng trong các bài toán. Thể tích được tính bằng diện tích đáy nhân với chiều cao của lăng trụ.
V = S.h =
Trong đó:
- V: Thể tích khối lăng trụ tam giác đều (đơn vị m³).
- S: Diện tích đáy (tam giác đều) (đơn vị m²).
- h: Chiều cao khối lăng trụ tam giác đều (đơn vị m).
- a: Độ dài cạnh đáy của tam giác đều.
4. Công Thức Tính Diện Tích Khối Lăng Trụ Tam Giác Đều
Để tính thể tích của khối lăng trụ tam giác đều, ta cần nắm vững cách tính diện tích xung quanh và diện tích toàn phần.
4.1. Diện Tích Xung Quanh
Diện tích xung quanh của lăng trụ tam giác đều bằng tổng diện tích các mặt bên, hoặc bằng chu vi đáy nhân với chiều cao.
Sxq = P.h = 3ah
Trong đó:
- P: Chu vi đáy (tam giác đều).
- h: Chiều cao lăng trụ.
- a: Độ dài cạnh đáy.
4.2. Diện Tích Toàn Phần
Diện tích toàn phần của khối lăng trụ tam giác đều bằng tổng diện tích xung quanh và diện tích hai đáy.
Stp = Sxq + 2Sđáy = 3ah +
Trong đó:
- Sxq: Diện tích xung quanh.
- Sđáy: Diện tích một đáy (tam giác đều).
- a: Độ dài cạnh đáy.
- h: Chiều cao lăng trụ.
5. Bài Tập Vận Dụng Tính Thể Tích Lăng Trụ Tam Giác Đều
Để củng cố kiến thức về thể tích của khối lăng trụ tam giác đều, hãy cùng luyện tập với các bài tập sau:
Bài 1: Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy AB = 4cm và chiều cao AA’ = 5cm. Tính thể tích của khối lăng trụ.
Giải:
- Diện tích đáy (tam giác đều): S =
- Thể tích khối lăng trụ: V = S.h =
Bài 2: Một khối lăng trụ tam giác đều có thể tích là và cạnh đáy bằng 6cm. Tính chiều cao của lăng trụ.
Giải:
- Diện tích đáy (tam giác đều): S =
- Chiều cao của lăng trụ: h = V/S =
Bài 3: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng 3a.
Giải:
- Diện tích đáy (tam giác đều): S =
- Chiều cao của lăng trụ: h = 3a
- Thể tích khối lăng trụ: V = S.h =
Hiểu rõ định nghĩa, tính chất và công thức tính thể tích của khối lăng trụ tam giác đều là chìa khóa để giải quyết các bài toán hình học không gian một cách hiệu quả. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin chinh phục mọi thử thách!