Trong chương trình hình học không gian THPT, Thể Tích Của Khối Chóp là một chủ đề quan trọng và thường xuyên xuất hiện trong các kỳ thi, đặc biệt là kỳ thi tốt nghiệp THPT. Việc nắm vững các kiến thức cơ bản và công thức tính thể tích khối chóp là yếu tố then chốt để đạt điểm cao. Bài viết này sẽ tổng hợp chi tiết các công thức tính thể tích khối chóp một cách dễ hiểu nhất, kèm theo các ví dụ minh họa và bài tập ứng dụng, giúp các em học sinh tự tin chinh phục mọi bài toán liên quan.
1. Lý Thuyết Nền Tảng Về Thể Tích Khối Chóp
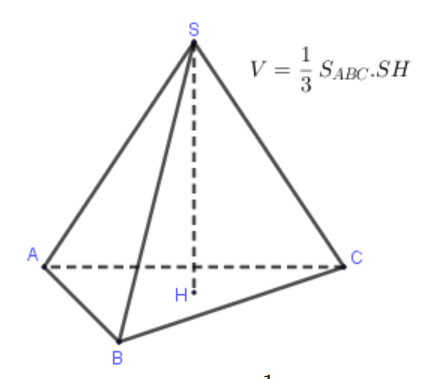
Thể tích của một vật thể là lượng không gian mà vật thể đó chiếm giữ. Đơn vị đo thể tích thường là mét khối (m³) hoặc centimet khối (cm³). Đối với khối chóp, thể tích được xác định dựa trên diện tích đáy và chiều cao của khối chóp.
Công thức tổng quát để tính thể tích khối chóp là:
V = (1/3) S h
Trong đó:
- V: Thể tích của khối chóp
- S: Diện tích đáy của khối chóp
- h: Chiều cao của khối chóp (khoảng cách từ đỉnh chóp đến mặt phẳng đáy)
Ngoài ra, trong các bài toán liên quan đến tỉ lệ thể tích của hai khối chóp tam giác, ta thường sử dụng công thức sau:
Nếu A’, B’, C’ lần lượt là các điểm nằm trên các cạnh SA, SB, SC của hình chóp tam giác S.ABC, thì:
2. Các Công Thức Tính Thể Tích Khối Chóp Thông Dụng
Dưới đây là tổng hợp các công thức tính thể tích khối chóp thường gặp và dễ áp dụng nhất:
2.1. Khối Chóp Có Mặt Bên Vuông Góc Với Đáy
Nếu khối chóp có một hoặc nhiều mặt bên vuông góc với mặt đáy, đường cao của khối chóp thường là đường cao của tam giác vuông góc với đáy hoặc là giao tuyến của các mặt bên vuông góc với đáy.
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a. Mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB = 2a√3 và góc (SBC) = 30º. Tính thể tích khối chóp S.ABC.
2.2. Khối Chóp Có Cạnh Bên Vuông Góc Với Đáy
Trong trường hợp này, cạnh bên vuông góc với đáy chính là chiều cao của khối chóp.
Ví dụ: Cho khối chóp S.ABC có SA vuông góc với đáy, SA = 4, AB = 6, BC = 10 và CA = 8. Tính thể tích khối chóp S.ABC.
2.3. Khối Chóp S.ABCD Có Đáy Là Hình Vuông
Nếu đáy của khối chóp là hình vuông, việc tính diện tích đáy trở nên đơn giản hơn.
Ví dụ: Cho khối chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và SC tạo với mặt phẳng (SAB) một góc 30 độ. Tính thể tích khối chóp.
2.4. Thể Tích Khối Chóp Lập Phương
Khối lập phương là một trường hợp đặc biệt của khối chóp, với tất cả các mặt đều là hình vuông. Công thức tính thể tích khối lập phương là: V = a³, trong đó a là độ dài cạnh của hình lập phương.
2.5. Thể Tích Khối Chóp Lăng Trụ Tam Giác Đều
Khối lăng trụ tam giác đều là khối lăng trụ có đáy là tam giác đều.
Ví dụ: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a = 2 cm và chiều cao là h = 3 cm. Tính thể tích hình lăng trụ này.
2.6. Thể Tích Khối Chóp Lục Giác Đều
Khối chóp lục giác đều có đáy là hình lục giác đều.
Ví dụ: Một khối chóp lục giác đều, góc giữa cạnh bên và mặt đáy là 30 độ, cạnh đáy a. Tính thể tích V của khối chóp.
2.7. Công Thức Tính Thể Tích Khối Chóp Lăng Trụ
Thể tích của khối lăng trụ được tính bằng công thức: V = B * h, trong đó B là diện tích đáy và h là chiều cao.
2.8. Tính Thể Tích Khối Chóp Khi Biết 3 Cạnh Bên
Trong trường hợp biết độ dài các cạnh của khối tứ diện, ta có thể sử dụng công thức tổng quát để tính thể tích.
Ví dụ: Cho khối tứ diện ABCD có AB = CD = 8, AD = BC = 5 và AC = BD = 7. Thể tích khối tứ diện đã cho bằng bao nhiêu?
2.9. Tìm Thể Tích Khối Chóp Các Cạnh Đôi Một Vuông Góc
Nếu các cạnh bên của khối chóp đôi một vuông góc với nhau, việc tính thể tích trở nên đơn giản hơn.
Ví dụ: Cho tứ diện SABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Biết SA = 3a, SB = 4a, SC = 5a. Tính theo a thể tích V của khối tứ diện SABC.
2.10. Thể Tích Khối Chóp Tròn Xoay (Khối Nón)
Thể tích khối nón được tính bằng công thức: V = (1/3) π r² * h, trong đó r là bán kính đáy và h là chiều cao.
Ví dụ: Tính thể tích của một khối nón có bán kính đáy là 5cm và chiều cao là 12cm.
2.11. Tính Thể Tích Của Khối Chóp Tam Giác Đều
Khối chóp tam giác đều là khối chóp có đáy là tam giác đều và chân đường cao trùng với tâm của tam giác đều.
Ví dụ: Tính thể tích V của khối chóp tam giác đều SABC biết chiều cao hình chóp bằng h, góc SBA = a.
2.12. Công Thức Tính Thể Tích Khối Chóp Tứ Giác Đều Cạnh Đáy Bằng a
Khối chóp tứ giác đều là khối chóp có đáy là hình vuông và chân đường cao trùng với tâm của hình vuông.
Ví dụ: Tính thể tích khối chóp tứ giác đều V có tất cả các cạnh bằng a.
Hy vọng với những kiến thức và công thức đã được tổng hợp trong bài viết này, các em học sinh sẽ nắm vững cách tính thể tích khối chóp và tự tin giải quyết các bài tập liên quan. Chúc các em thành công trong học tập!