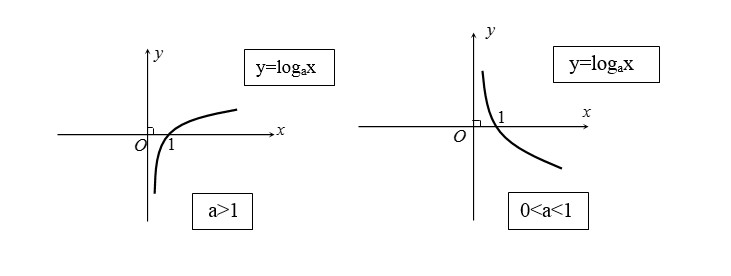Tập Xác Định Của Logarit: Lý Thuyết, Ví Dụ & Bài Tập

Để nắm vững kiến thức về hàm số logarit, việc hiểu rõ về Tập Xác định Của Logarit là vô cùng quan trọng. Bài viết này sẽ cung cấp cho bạn một cái nhìn toàn diện về vấn đề này, từ lý thuyết cơ bản đến các ví dụ minh họa và bài tập áp dụng, giúp bạn tự tin giải quyết mọi bài toán liên quan.

1. Tổng Quan Về Hàm Số Logarit

Hàm số logarit là một trong những hàm số cơ bản và quan trọng trong toán học. Nó có mối liên hệ mật thiết với hàm số mũ và được ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật.

• Định nghĩa: Cho số thực a > 0, a ≠ 1 và x > 0. Hàm số y = log_ax được gọi là hàm số logarit cơ số a.

• Tập xác định: Tập xác định của hàm số logarit y = log_ax là tập hợp tất cả các giá trị x > 0, ký hiệu là D = (0; +∞).

2. Điều Kiện Xác Định Của Hàm Số Logarit

Để hàm số logarit có nghĩa, biểu thức trong logarit phải thỏa mãn các điều kiện sau:

• Biểu thức dưới dấu logarit phải dương: Nếu hàm số có dạng y = log_au(x), thì điều kiện là u(x) > 0.
• Cơ số của logarit phải dương và khác 1: Nếu cơ số là một biểu thức chứa biến, ví dụ y = log_u(x)v(x), thì cần thêm điều kiện u(x) > 0, u(x) ≠ 1.

3. Các Bước Tìm Tập Xác Định Của Hàm Số Logarit

Để tìm tập xác định của một hàm số logarit cụ thể, ta thực hiện các bước sau:

1. Xác định dạng của hàm số: Xác định xem hàm số có dạng y = log_au(x) hay y = log_u(x)v(x).
2. Thiết lập các điều kiện: Dựa vào dạng hàm số, thiết lập các điều kiện cần thiết để hàm số có nghĩa.
3. Giải các bất phương trình: Giải các bất phương trình để tìm ra tập nghiệm của x.
4. Kết luận: Kết luận tập xác định của hàm số.

4. Ví Dụ Minh Họa

• Ví dụ 1: Tìm tập xác định của hàm số y = log₂(x – 3).

  • Điều kiện: x – 3 > 0
  • Giải: x > 3
  • Vậy tập xác định là D = (3; +∞).

• Ví dụ 2: Tìm tập xác định của hàm số y = log_x(5 – x).

  • Điều kiện:
    • x > 0
    • x ≠ 1
    • 5 – x > 0
  • Giải:
    • x > 0
    • x ≠ 1
    • x < 5
  • Vậy tập xác định là D = (0; 1) ∪ (1; 5).

5. Lưu Ý Quan Trọng Khi Tìm Tập Xác Định

• Kết hợp các điều kiện: Khi hàm số logarit có nhiều điều kiện, cần kết hợp tất cả các điều kiện để tìm ra tập xác định cuối cùng.
• Chú ý đến cơ số: Nếu cơ số của logarit là một biểu thức chứa biến, cần đảm bảo cơ số dương và khác 1.
• Kiểm tra lại kết quả: Sau khi tìm được tập xác định, nên kiểm tra lại bằng cách thay một vài giá trị trong tập xác định vào hàm số để đảm bảo hàm số có nghĩa.

6. Bài Tập Vận Dụng

Để củng cố kiến thức, hãy thử sức với các bài tập sau:

1. Tìm tập xác định của hàm số y = log₃(x² – 4).
2. Tìm tập xác định của hàm số y = log_(x+1)(2x – 1).
3. Tìm tập xác định của hàm số y = log_0.5(9 – x²).

7. Ứng Dụng Của Tập Xác Định Trong Giải Toán

Việc xác định đúng tập xác định của hàm số logarit là bước quan trọng để giải các bài toán liên quan đến:

• Tìm nghiệm của phương trình logarit: Chỉ những nghiệm thuộc tập xác định mới là nghiệm hợp lệ.
• Khảo sát sự biến thiên của hàm số logarit: Tập xác định là cơ sở để xác định khoảng đồng biến, nghịch biến của hàm số.
• Giải các bài toán thực tế: Nhiều bài toán thực tế liên quan đến logarit đòi hỏi phải xác định tập xác định để đảm bảo kết quả có ý nghĩa.

8. Kết Luận

Nắm vững kiến thức về tập xác định của logarit là chìa khóa để giải quyết các bài toán liên quan đến hàm số logarit một cách chính xác và hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích để chinh phục các bài toán về logarit. Chúc bạn thành công!