Trong toán học, đặc biệt là khi nghiên cứu về hàm số, hai khái niệm quan trọng mà chúng ta cần nắm vững là tập xác định và tập giá trị. Bài viết này sẽ tập trung làm rõ “Tập Giá Trị Là Gì” một cách chi tiết, dễ hiểu, kèm theo ví dụ minh họa.
1. Định Nghĩa Tập Giá Trị
Cho hàm số (y = f(x)), trong đó (x) thuộc tập xác định (D).
Tập giá trị (Range) của hàm số (y = f(x)) là tập hợp tất cả các giá trị (y) mà hàm số nhận được khi (x) chạy khắp tập xác định (D). Nói cách khác, đó là tập hợp tất cả các (f(x)) sao cho (x in D).
Ký hiệu: Tập giá trị thường được ký hiệu là (T) hoặc (R) (Range).
Mối quan hệ giữa tập xác định và tập giá trị:
- Tập xác định (D) là tập hợp các giá trị đầu vào (input) mà hàm số có thể nhận.
- Tập giá trị (T) là tập hợp các giá trị đầu ra (output) tương ứng với các giá trị đầu vào trong tập xác định.
Ví dụ minh họa:
Xét hàm số (y = x^2) với tập xác định (D = mathbb{R}) (tất cả các số thực). Vì bình phương của một số thực luôn lớn hơn hoặc bằng 0, tập giá trị của hàm số là (T = [0; +infty)) (tất cả các số thực không âm).
2. Cách Tìm Tập Giá Trị
Việc tìm tập giá trị của một hàm số phụ thuộc vào dạng của hàm số đó. Dưới đây là một số phương pháp phổ biến:
-
Dựa vào bảng giá trị: Nếu hàm số được cho dưới dạng bảng giá trị, tập giá trị là tập hợp các giá trị (y) có trong bảng.
Ví dụ: Bảng giá trị cho một hàm số như sau:
x -2 -1 0 1 2 y 4 1 0 1 4 Vậy tập giá trị của hàm số là (T = {0, 1, 4}).
-
Dựa vào đồ thị: Nếu có đồ thị của hàm số, tập giá trị là tập hợp tất cả các giá trị (y) mà đồ thị hàm số bao phủ trên trục tung (trục (y)). Để xác định tập giá trị trên đồ thị, ta chiếu tất cả các điểm trên đồ thị xuống trục Oy, phần trục Oy bị phủ bởi hình chiếu chính là tập giá trị.
Ví dụ:
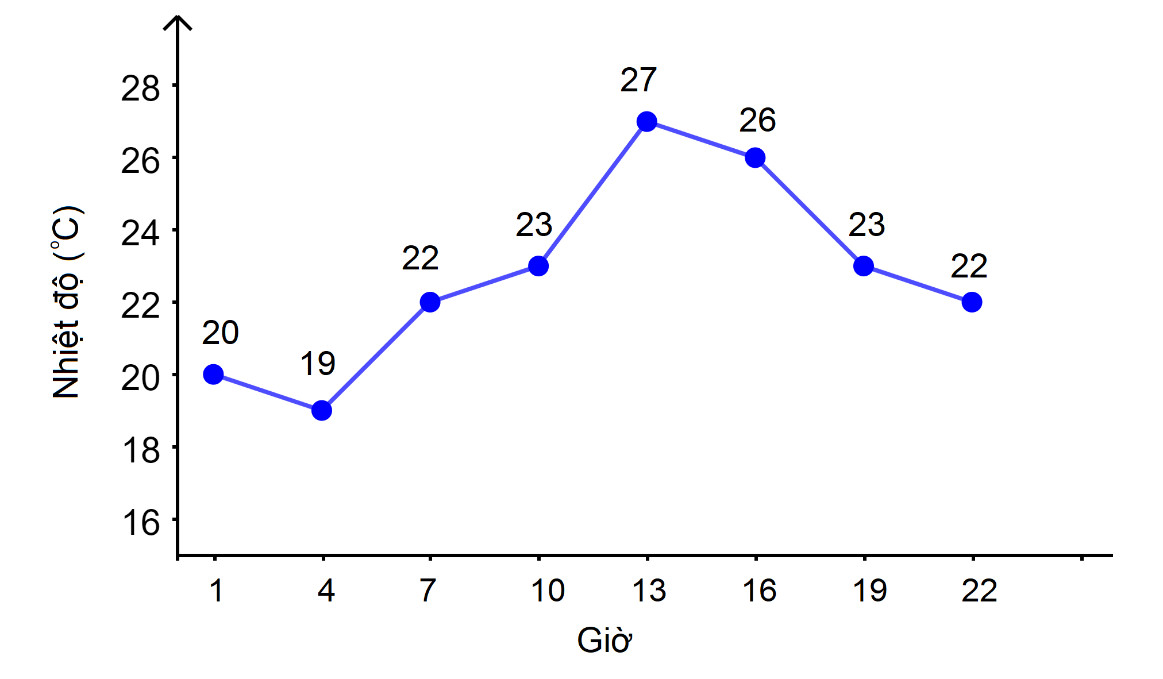Đồ thị hàm số minh họa tập giá trị trên trục tungTrong ví dụ dự báo thời tiết, tập giá trị biểu diễn các mức nhiệt độ khác nhau trong ngày.
-
Dựa vào công thức:
- Hàm số bậc nhất: (y = ax + b) ((a ne 0)) có tập giá trị là (T = mathbb{R}) (tất cả các số thực).
- Hàm số bậc hai: (y = ax^2 + bx + c) ((a ne 0)). Để tìm tập giá trị, ta tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số (tọa độ đỉnh của parabol).
- Nếu (a > 0), hàm số có giá trị nhỏ nhất là (y{min} = -frac{Delta}{4a}), và tập giá trị là (T = [y{min}; +infty)).
- Nếu (a < 0), hàm số có giá trị lớn nhất là (y{max} = -frac{Delta}{4a}), và tập giá trị là (T = (-infty; y{max}]).
- Hàm số lượng giác: Sử dụng tính chất của các hàm số sin, cos, tan, cot. Ví dụ:
- Hàm số (y = sin(x)) có tập giá trị là (T = [-1; 1]).
- Hàm số (y = cos(x)) có tập giá trị là (T = [-1; 1]).
- Hàm số chứa căn thức: Xét điều kiện để biểu thức dưới căn không âm, sau đó đánh giá giá trị của biểu thức căn thức.
Ví dụ: Hàm số (y = sqrt{x}) với (x ge 0) có tập giá trị là (T = [0; +infty)). - Hàm số phân thức: Tìm tập xác định, sau đó xét giới hạn của hàm số khi (x) tiến tới các điểm đặc biệt (vô cùng, các điểm mà hàm số không xác định) để xác định tập giá trị.
3. Ví dụ Cụ Thể
Ví dụ 1: Tìm tập giá trị của hàm số (y = x^2 – 4x + 3).
- Bước 1: Xác định hệ số: (a = 1, b = -4, c = 3). Vì (a > 0), hàm số có giá trị nhỏ nhất.
- Bước 2: Tìm giá trị nhỏ nhất: (Delta = b^2 – 4ac = (-4)^2 – 4 1 3 = 4).
Vậy (y_{min} = -frac{Delta}{4a} = -frac{4}{4*1} = -1). - Bước 3: Kết luận: Tập giá trị của hàm số là (T = [-1; +infty)).
Ví dụ 2: Tìm tập giá trị của hàm số (y = frac{1}{x-2}).
- Bước 1: Tìm tập xác định: (D = mathbb{R} setminus {2}) (tất cả các số thực trừ 2).
- Bước 2: Xét giới hạn:
- Khi (x to 2^+), (y to +infty).
- Khi (x to 2^-), (y to -infty).
- Khi (x to +infty), (y to 0).
- Khi (x to -infty), (y to 0).
- Bước 3: Kết luận: Tập giá trị của hàm số là (T = mathbb{R} setminus {0}) (tất cả các số thực trừ 0).
Kết luận:
Hiểu rõ “tập giá trị là gì” và cách tìm tập giá trị là kiến thức quan trọng trong giải toán và ứng dụng toán học. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về khái niệm này. Việc luyện tập giải các bài tập khác nhau sẽ giúp bạn nắm vững kiến thức hơn.
