Bài viết này sẽ tập trung vào việc xác định tập giá trị của hàm số lượng giác y = sin2x + √3cos2x + 1. Đây là một dạng bài tập thường gặp trong chương trình Toán phổ thông và các kỳ thi quan trọng. Chúng ta sẽ đi sâu vào phương pháp giải và các ví dụ minh họa.
Để tìm tập giá trị của hàm số, chúng ta cần biến đổi hàm số về dạng đơn giản hơn, dễ xác định giá trị lớn nhất và giá trị nhỏ nhất.
Hàm số đã cho có dạng:
y = sin2x + √3cos2x + 1
Ta nhận thấy phần sin2x + √3cos2x có dạng asin2x + bcos2x. Chúng ta có thể đưa biểu thức này về dạng lượng giác bằng cách chia và nhân với √(a² + b²).
Trong trường hợp này, a = 1 và b = √3, suy ra √(a² + b²) = √(1² + (√3)²) = √(1 + 3) = √4 = 2.
Vậy ta viết lại hàm số như sau:
y = 2(1/2 * sin2x + √3/2 * cos2x) + 1
Nhận thấy 1/2 = cos(π/3) và √3/2 = sin(π/3), ta có thể viết lại biểu thức trong ngoặc như sau:
y = 2(cos(π/3) * sin2x + sin(π/3) * cos2x) + 1
Áp dụng công thức cộng góc sin(a + b) = sin(a)cos(b) + cos(a)sin(b), ta có:
y = 2sin(2x + π/3) + 1
Bây giờ hàm số đã được đưa về dạng đơn giản hơn. Ta biết rằng giá trị của hàm sin luôn nằm trong đoạn [-1; 1]. Do đó:
-1 ≤ sin(2x + π/3) ≤ 1
Nhân cả ba vế của bất đẳng thức với 2:
-2 ≤ 2sin(2x + π/3) ≤ 2
Cộng cả ba vế của bất đẳng thức với 1:
-2 + 1 ≤ 2sin(2x + π/3) + 1 ≤ 2 + 1
-1 ≤ y ≤ 3
Vậy, tập giá trị của hàm số y = sin2x + √3cos2x + 1 là đoạn [-1; 3]. Giá trị nhỏ nhất của hàm số là -1 và giá trị lớn nhất là 3.
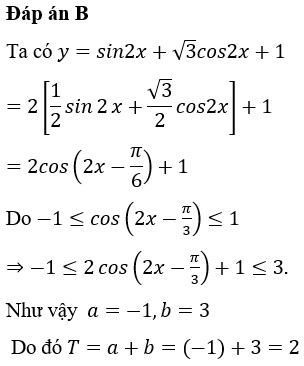Lời giải chi tiết bài toán tìm tập giá trị của hàm số lượng giác y=sin2x+√3cos2x+1
Hình ảnh minh họa cách giải bài toán tìm tập giá trị của hàm số y=sin2x+√3cos2x+1, tập trung vào việc biến đổi lượng giác và xác định khoảng giá trị.
Tổng quát:
Để tìm tập giá trị của hàm số dạng y = asin(kx) + bcos(kx) + c, ta thực hiện các bước sau:
- Biến đổi về dạng
Rsin(kx + φ) + c: TìmR = √(a² + b²). Sử dụng các công thức lượng giác để biến đổi. - Xác định khoảng giá trị của sin(kx + φ): Luôn nằm trong đoạn
[-1; 1]. - Suy ra khoảng giá trị của y: Nhân và cộng các vế của bất đẳng thức để tìm ra khoảng giá trị của y.
Ví dụ:
Tìm tập giá trị của hàm số y = 3sin4x - 4cos4x + 5.
R = √(3² + (-4)²) = √(9 + 16) = √25 = 5.y = 5(3/5 * sin4x - 4/5 * cos4x) + 5. Đặtcosφ = 3/5vàsinφ = 4/5.y = 5(cosφ * sin4x - sinφ * cos4x) + 5 = 5sin(4x - φ) + 5.-1 ≤ sin(4x - φ) ≤ 1-5 ≤ 5sin(4x - φ) ≤ 50 ≤ 5sin(4x - φ) + 5 ≤ 10
Vậy tập giá trị của hàm số là đoạn [0; 10].
Việc nắm vững các công thức lượng giác và kỹ năng biến đổi là rất quan trọng để giải quyết các bài toán tìm tập giá trị của hàm số. Hy vọng bài viết này cung cấp cho bạn những kiến thức hữu ích.
