Trong toán học, khái niệm Tập Con Của Tập Hợp đóng vai trò nền tảng và xuất hiện rộng rãi trong nhiều lĩnh vực khác nhau. Hiểu rõ về tập con không chỉ giúp bạn nắm vững kiến thức cơ bản về lý thuyết tập hợp, mà còn mở ra cánh cửa khám phá những ứng dụng thú vị trong các bài toán thực tế và khoa học máy tính.
Định nghĩa Tập Con
Một tập hợp A được gọi là tập con của tập hợp B nếu mọi phần tử của A đều đồng thời là phần tử của B. Nói cách khác, nếu bạn tìm thấy bất kỳ phần tử nào thuộc A mà không thuộc B, thì A không phải là tập con của B.
Ký Hiệu
Chúng ta sử dụng ký hiệu (A subseteq B) (đọc là “A là tập con của B” hoặc “A chứa trong B”) để biểu thị mối quan hệ tập con. Ngoài ra, ký hiệu (B supseteq A) (đọc là “B chứa A”) cũng được sử dụng với ý nghĩa tương tự.
Ví dụ:
Cho tập hợp (A = {1, 2, 3}) và (B = {1, 2, 3, 4, 5}). Vì tất cả các phần tử của A (1, 2 và 3) đều thuộc B, nên A là một tập con của B. Ta viết (A subseteq B).
Các Trường Hợp Đặc Biệt và Tính Chất Quan Trọng
-
Tập Rỗng: Tập rỗng (ký hiệu là (emptyset)) là tập hợp không chứa bất kỳ phần tử nào. Tập rỗng là tập con của mọi tập hợp. Tức là, với mọi tập A, ta luôn có (emptyset subseteq A).
-
Tập Hợp Bằng Chính Nó: Mọi tập hợp đều là tập con của chính nó. Với mọi tập A, ta có (A subseteq A).
-
Quan Hệ Bao Hàm: Nếu A là tập con của B, ta nói rằng A và B có quan hệ bao hàm.
-
Không Phải Tập Con: Nếu A không phải là tập con của B, ta ký hiệu là (A nsubseteq B). Điều này có nghĩa là tồn tại ít nhất một phần tử trong A không thuộc B.
Số Lượng Tập Con
Một câu hỏi tự nhiên đặt ra là: một tập hợp cho trước có bao nhiêu tập con? Câu trả lời là: Nếu tập hợp A có n phần tử, thì số lượng tập con của A là (2^n).
Ví dụ:
Cho tập hợp (A = {a, b, c}). Tập A có 3 phần tử, vậy số tập con của A là (2^3 = 8). Các tập con đó là:
- (emptyset)
- ({a})
- ({b})
- ({c})
- ({a, b})
- ({a, c})
- ({b, c})
- ({a, b, c})
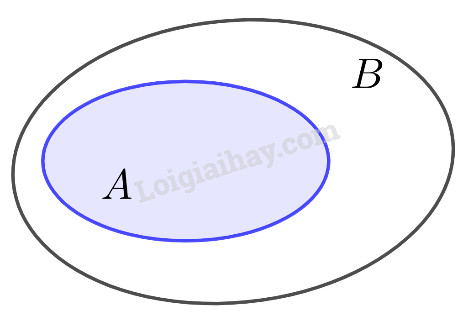
Biểu Đồ Ven Minh Họa Tập Con
Biểu đồ Ven là một công cụ trực quan hữu ích để biểu diễn các tập hợp và mối quan hệ giữa chúng. Trong biểu đồ Ven, mỗi tập hợp được biểu diễn bằng một hình tròn hoặc hình elip.
Hình trên minh họa tập A là tập con của tập B. Vòng tròn biểu diễn tập A nằm hoàn toàn bên trong vòng tròn biểu diễn tập B, thể hiện rằng mọi phần tử của A đều thuộc B.
Mối Quan Hệ Giữa Các Tập Hợp Số
Các tập hợp số thường gặp như tập số tự nhiên ((mathbb{N})), tập số nguyên ((mathbb{Z})), tập số hữu tỷ ((mathbb{Q})) và tập số thực ((mathbb{R})) có mối quan hệ bao hàm lẫn nhau:
(mathbb{N} subset mathbb{Z} subset mathbb{Q} subset mathbb{R})
Điều này có nghĩa là mọi số tự nhiên đều là số nguyên, mọi số nguyên đều là số hữu tỷ và mọi số hữu tỷ đều là số thực.
Kiểm Tra Một Tập Hợp Có Phải Là Tập Con
Để kiểm tra xem A có phải là tập con của B hay không, ta cần chứng minh rằng:
(A subseteq B Leftrightarrow forall x in A Rightarrow x in B)
Điều này có nghĩa là “với mọi x thuộc A, x cũng thuộc B”. Ngược lại, để chứng minh A không phải là tập con của B, ta chỉ cần tìm một phần tử x thuộc A nhưng không thuộc B:
(A nsubseteq B Leftrightarrow exists x in A: x notin B)
Định Nghĩa Hai Tập Hợp Bằng Nhau
Hai tập hợp A và B được gọi là bằng nhau nếu chúng có cùng các phần tử. Nói cách khác, A và B bằng nhau nếu A là tập con của B và B cũng là tập con của A.
Ký Hiệu: (A = B)
Điều kiện tương đương: (A = B Leftrightarrow begin{cases} A subseteq B B subseteq A end{cases})
Ví dụ:
Cho C là tập hợp các hình thoi có hai đường chéo bằng nhau và D là tập hợp các hình vuông. Khi đó, (C subseteq D) và (D subseteq C) nên C = D.
Ứng Dụng của Tập Con
Khái niệm tập con được sử dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Cơ sở dữ liệu: Trong cơ sở dữ liệu, tập con được sử dụng để định nghĩa các truy vấn con và các quan hệ giữa các bảng.
- Lý thuyết đồ thị: Trong lý thuyết đồ thị, tập con được sử dụng để định nghĩa các đồ thị con và các thành phần liên thông.
- Khoa học máy tính: Trong khoa học máy tính, tập con được sử dụng để định nghĩa các kiểu dữ liệu, các thuật toán và các cấu trúc dữ liệu.
Hiểu rõ về tập con của tập hợp là rất quan trọng để xây dựng nền tảng vững chắc trong toán học và các lĩnh vực liên quan. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về khái niệm này.
Alt text: Biểu đồ Ven minh họa hai tập hợp có phần tử chung, thể hiện sự giao nhau giữa hai tập.