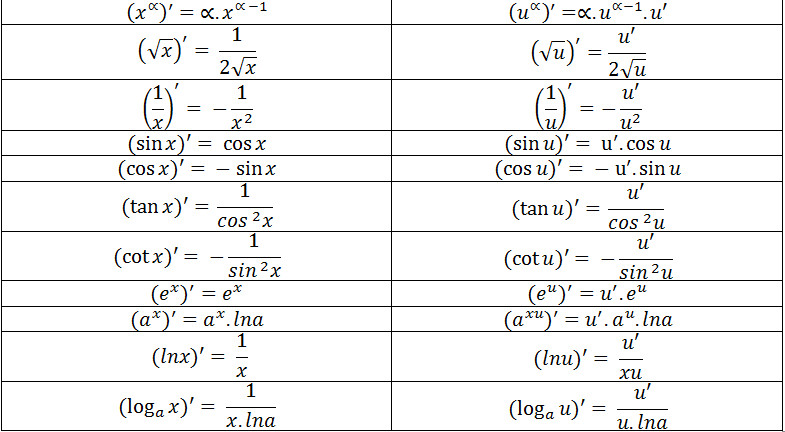Định Nghĩa và Ý Nghĩa của Đạo Hàm
Đạo hàm của một hàm số đo lường sự thay đổi tức thời của hàm số đó tại một điểm. Nó biểu thị tốc độ thay đổi của hàm số và là một công cụ cơ bản trong giải tích. Về mặt hình học, đạo hàm tại một điểm là độ dốc của đường tiếp tuyến với đồ thị hàm số tại điểm đó.
Cho hàm số y = f(x) xác định trên một khoảng (a, b) và x₀ ∈ (a, b), đạo hàm của f(x) tại x₀, ký hiệu f'(x₀), được định nghĩa là:
f'(x₀) = lim (x→x₀) [f(x) – f(x₀)] / (x – x₀)
Nếu giới hạn này tồn tại và hữu hạn.
Đạo Hàm của Hàm Tang (tan x)
Hàm tang (tan x) là một hàm lượng giác quan trọng, được định nghĩa là tỷ số giữa sin x và cos x:
tan x = sin x / cos x
Để tìm “Tan X đạo Hàm”, chúng ta sử dụng quy tắc đạo hàm của thương:
Nếu y = u(x) / v(x), thì y’ = (u’v – uv’) / v²
Trong trường hợp tan x, ta có:
u(x) = sin x, u'(x) = cos x
v(x) = cos x, v'(x) = -sin x
Áp dụng công thức đạo hàm của thương:
(tan x)’ = (cos x cos x – sin x (-sin x)) / (cos x)²
= (cos²x + sin²x) / cos²x
= 1 / cos²x
Vậy, đạo hàm của tan x là:
(tan x)’ = 1 / cos²x = sec²x
Trong đó, sec x = 1 / cos x là hàm secant.
Tổng Hợp Công Thức Đạo Hàm Các Hàm Số Cơ Bản
Để hiểu rõ hơn về đạo hàm của tan x, cùng ôn lại các công thức đạo hàm của các hàm số cơ bản:
Alt text: Bảng tổng hợp công thức đạo hàm của các hàm số thường gặp, bao gồm đạo hàm của hàm lũy thừa, hàm số mũ, hàm logarit và các hàm lượng giác cơ bản để học sinh dễ dàng tra cứu.
Đạo Hàm của tan u (Hàm Hợp)
Khi tính đạo hàm của hàm hợp tan u, với u = u(x) là một hàm của x, ta sử dụng quy tắc chuỗi (chain rule):
(tan u)’ = (du/dx) (1 / cos²u) = u’ / cos²u = u’ sec²u
Ví dụ: Nếu y = tan(x² + 1), thì:
u(x) = x² + 1
u'(x) = 2x
Do đó:
y’ = (tan(x² + 1))’ = 2x / cos²(x² + 1) = 2x * sec²(x² + 1)
Ứng Dụng của Đạo Hàm tan x
Đạo hàm của tan x có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực liên quan:
- Tìm cực trị của hàm số: Đạo hàm giúp xác định các điểm cực đại và cực tiểu của hàm số.
- Khảo sát và vẽ đồ thị hàm số: Đạo hàm cung cấp thông tin về chiều biến thiên, tính đơn điệu và hình dạng của đồ thị hàm số.
- Giải các bài toán liên quan đến tốc độ và gia tốc: Trong vật lý, đạo hàm được sử dụng để tính vận tốc và gia tốc của một vật chuyển động.
- Tối ưu hóa: Đạo hàm được sử dụng để tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số, có ứng dụng trong nhiều lĩnh vực như kinh tế, kỹ thuật.
Công Thức Đạo Hàm Các Hàm Lượng Giác
Để nắm vững hơn về đạo hàm của các hàm lượng giác, ta xem xét bảng công thức sau:
- (sin x)’ = cos x
- (cos x)’ = -sin x
- (tan x)’ = 1 / cos²x = sec²x
- (cot x)’ = -1 / sin²x = -csc²x
- (sec x)’ = sec x * tan x
- (csc x)’ = -csc x * cot x
Ví Dụ Minh Họa
Ví dụ 1: Tính đạo hàm của hàm số y = 3tan(2x).
Giải:
Sử dụng công thức đạo hàm của hàm hợp:
y’ = 3 (tan(2x))’ = 3 (2 / cos²(2x)) = 6 / cos²(2x) = 6sec²(2x)
Ví dụ 2: Tính đạo hàm của hàm số y = x² * tan x.
Giải:
Sử dụng quy tắc đạo hàm của tích: (uv)’ = u’v + uv’
y’ = (x²)’ tan x + x² (tan x)’
= 2x tan x + x² (1 / cos²x)
= 2x tan x + x² sec²x
Bài Tập Tự Luyện
- Tìm đạo hàm của hàm số y = tan(x³) + 5x.
- Tính đạo hàm của hàm số y = sin x * tan x.
- Tìm đạo hàm của hàm số y = √(tan x).
- Cho hàm số f(x) = tan²(x). Tính f'(π/4).
Đạo Hàm Cấp Cao
Đạo hàm cấp cao là đạo hàm của đạo hàm. Ví dụ, đạo hàm cấp hai là đạo hàm của đạo hàm cấp nhất.
Bảng công thức đạo hàm cấp cao thường gặp
Alt text: Bảng tổng hợp các công thức đạo hàm cấp cao thường gặp của các hàm số cơ bản như hàm đa thức, hàm lượng giác và hàm mũ, giúp học sinh ôn tập và áp dụng trong các bài toán phức tạp.
Ví dụ: Tính đạo hàm cấp hai của y = tan x.
Ta đã biết y’ = 1 / cos²x = sec²x
Để tính y”, ta có thể viết sec²x = (cos x)⁻² và sử dụng quy tắc chuỗi:
y” = -2(cos x)⁻³ (-sin x) = 2sin x / cos³x = 2tan x sec²x
Kết Luận
Bài viết này đã cung cấp một cái nhìn tổng quan và chi tiết về “tan x đạo hàm”, bao gồm công thức, cách tính, ứng dụng và ví dụ minh họa. Hy vọng rằng, với những kiến thức này, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến đạo hàm của hàm tang và các hàm lượng giác khác.