Tam thức bậc hai là một khái niệm quan trọng trong chương trình Toán học lớp 10. Việc nắm vững lý thuyết và các dạng bài tập liên quan sẽ giúp học sinh giải quyết tốt các bài toán và ứng dụng vào thực tế. Bài viết này sẽ tổng hợp kiến thức về tam thức bậc hai, các dạng toán thường gặp và phương pháp giải chi tiết.
1. Định nghĩa tam thức bậc hai
Tam thức bậc hai đối với biến x là biểu thức có dạng:
(f(x) = ax^2 + bx + c)
trong đó a, b, c là các hệ số, và (a ne 0).
2. Nghiệm của tam thức bậc hai
Nghiệm của tam thức bậc hai (f(x) = ax^2 + bx + c) là các giá trị của x sao cho (f(x) = 0). Để tìm nghiệm, ta giải phương trình bậc hai:
(ax^2 + bx + c = 0)
Sử dụng công thức nghiệm:
-
Tính (Delta = b^2 – 4ac)
-
Nếu (Delta > 0): Phương trình có hai nghiệm phân biệt:
(x_1 = frac{-b + sqrt{Delta}}{2a}) và (x_2 = frac{-b – sqrt{Delta}}{2a})
-
Nếu (Delta = 0): Phương trình có nghiệm kép:
(x_1 = x_2 = frac{-b}{2a})
-
Nếu (Delta < 0): Phương trình vô nghiệm.
3. Xét dấu tam thức bậc hai
Việc xét dấu tam thức bậc hai giúp xác định khoảng giá trị của x mà tại đó tam thức mang giá trị dương, âm hoặc bằng 0.
-
Trường hợp (Delta > 0): Tam thức có hai nghiệm phân biệt (x_1) và (x_2) ((x_1 < x_2)).
- (f(x) > 0) khi (x < x_1) hoặc (x > x_2) (cùng dấu với hệ số a)
- (f(x) < 0) khi (x_1 < x < x_2) (trái dấu với hệ số a)
- (f(x) = 0) khi (x = x_1) hoặc (x = x_2)
-
Trường hợp (Delta = 0): Tam thức có nghiệm kép (x = frac{-b}{2a}).
- (f(x)) cùng dấu với a với mọi (x ne frac{-b}{2a})
- (f(x) = 0) khi (x = frac{-b}{2a})
-
Trường hợp (Delta < 0): Tam thức luôn cùng dấu với hệ số a với mọi x.
- (f(x) > 0) với mọi x nếu (a > 0)
- (f(x) < 0) với mọi x nếu (a < 0)
Hình ảnh minh họa bảng xét dấu tam thức bậc hai với nghiệm x1 và x2, thể hiện sự thay đổi dấu của tam thức dựa trên giá trị của x so với nghiệm.
4. Các dạng toán liên quan đến tam thức bậc hai
- Giải bất phương trình bậc hai: Dựa vào việc xét dấu tam thức bậc hai để tìm tập nghiệm của bất phương trình.
- Tìm điều kiện để tam thức bậc hai luôn dương hoặc luôn âm: Sử dụng điều kiện về dấu của hệ số a và (Delta).
- Bài toán chứa tham số: Tìm giá trị của tham số để tam thức bậc hai thỏa mãn một điều kiện nào đó (ví dụ: có nghiệm, vô nghiệm, luôn dương, luôn âm…).
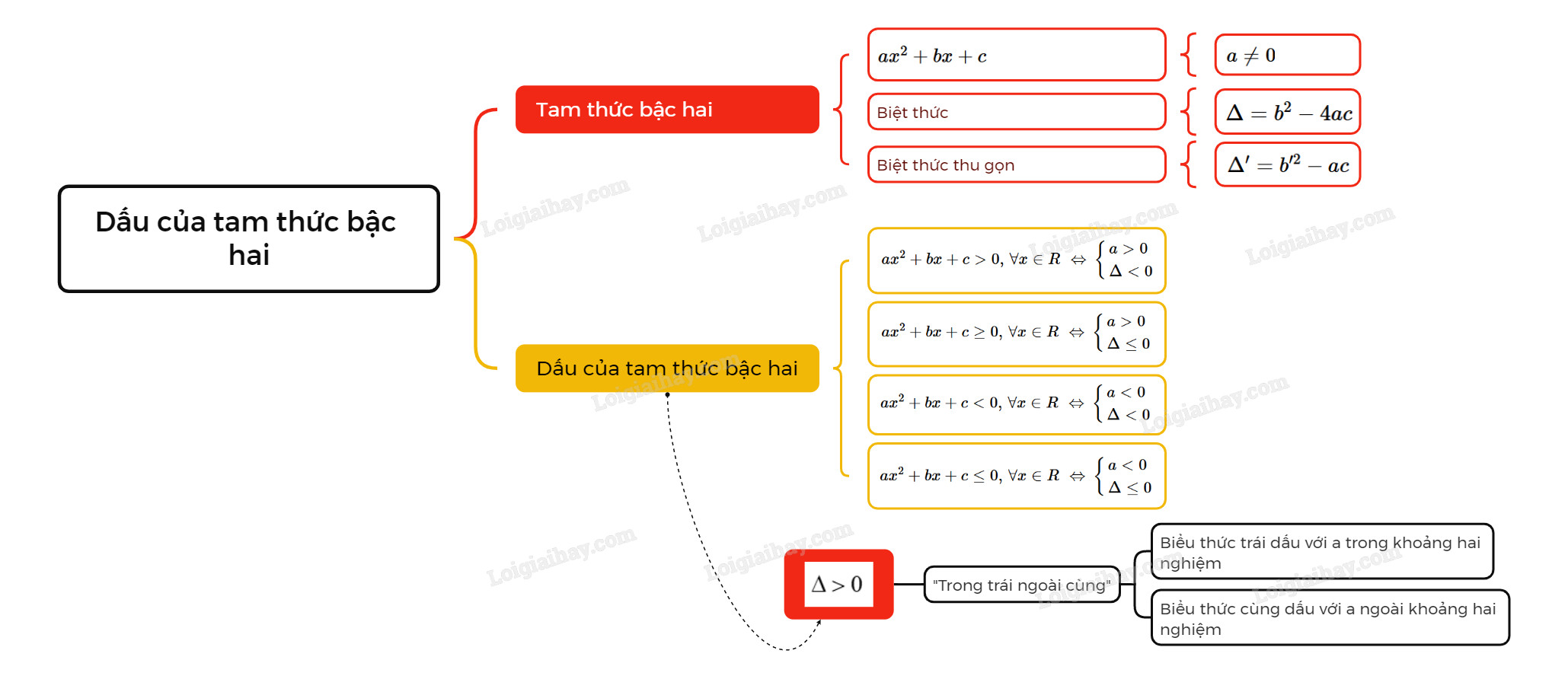
5. Điều kiện để tam thức bậc hai luôn dương hoặc luôn âm
Cho tam thức bậc hai (f(x) = ax^2 + bx + c)
- (f(x) > 0, forall x in mathbb{R} Leftrightarrow begin{cases} a > 0 Delta < 0 end{cases})
- (f(x) ge 0, forall x in mathbb{R} Leftrightarrow begin{cases} a > 0 Delta le 0 end{cases})
- (f(x) < 0, forall x in mathbb{R} Leftrightarrow begin{cases} a < 0 Delta < 0 end{cases})
- (f(x) le 0, forall x in mathbb{R} Leftrightarrow begin{cases} a < 0 Delta le 0 end{cases})
6. Bài tập vận dụng
Bài 1: Xét dấu tam thức (f(x) = -2x^2 + 3x – 1)
Giải:
Phương trình (-2x^2 + 3x – 1 = 0) có (Delta = 3^2 – 4(-2)(-1) = 1 > 0), vậy phương trình có hai nghiệm phân biệt:
(x_1 = frac{-3 + sqrt{1}}{-4} = frac{1}{2}) và (x_2 = frac{-3 – sqrt{1}}{-4} = 1)
Vì a = -2 < 0, ta có bảng xét dấu:
| x | -(infty) | 1/2 | 1 | +(infty) |
|---|---|---|---|---|
| f(x) | – | 0 | 0 | – |
| + |
Vậy:
- (f(x) > 0) khi (x in (frac{1}{2}; 1))
- (f(x) < 0) khi (x in (-infty; frac{1}{2}) cup (1; +infty))
- (f(x) = 0) khi (x = frac{1}{2}) hoặc (x = 1)
Bài 2: Tìm m để tam thức (f(x) = x^2 – 2mx + m + 2 > 0, forall x in mathbb{R})
Giải:
Để (f(x) > 0) với mọi x, ta cần:
(begin{cases} a > 0 Delta’ < 0 end{cases})
Ta có: (a = 1 > 0) (luôn đúng)
(Delta’ = (-m)^2 – (m + 2) = m^2 – m – 2 < 0)
Giải bất phương trình (m^2 – m – 2 < 0):
Phương trình (m^2 – m – 2 = 0) có hai nghiệm (m_1 = -1) và (m_2 = 2)
Vậy (m^2 – m – 2 < 0) khi (m in (-1; 2))
Kết luận: Để (f(x) > 0) với mọi x, thì (m in (-1; 2)).
 Đồ thị minh họa sự tương quan giữa đường cong bậc hai và trục hoành
Đồ thị minh họa sự tương quan giữa đường cong bậc hai và trục hoành
Hình ảnh đồ thị hàm số bậc hai minh họa các trường hợp tương giao với trục hoành, giúp hình dung trực quan về nghiệm và dấu của tam thức bậc hai.
7. Kết luận
Tam thức bậc hai là một phần kiến thức quan trọng và có nhiều ứng dụng trong toán học. Việc nắm vững lý thuyết, các dạng bài tập và phương pháp giải sẽ giúp học sinh tự tin hơn khi đối mặt với các bài toán liên quan. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về tam thức bậc hai lớp 10.

