Trong hình học phẳng, tam giác cân đóng vai trò quan trọng, đặc biệt khi xét đến các đường đặc biệt như đường trung tuyến. Bài viết này sẽ đi sâu vào khái niệm “Tam Giác Cân Có đường Trung Tuyến”, làm rõ các tính chất, định lý liên quan và cung cấp bài tập vận dụng để củng cố kiến thức.
Đường Trung Tuyến Của Tam Giác Cân Là Gì?
Đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác đó đến trung điểm của cạnh đối diện. Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh cân có những tính chất đặc biệt.
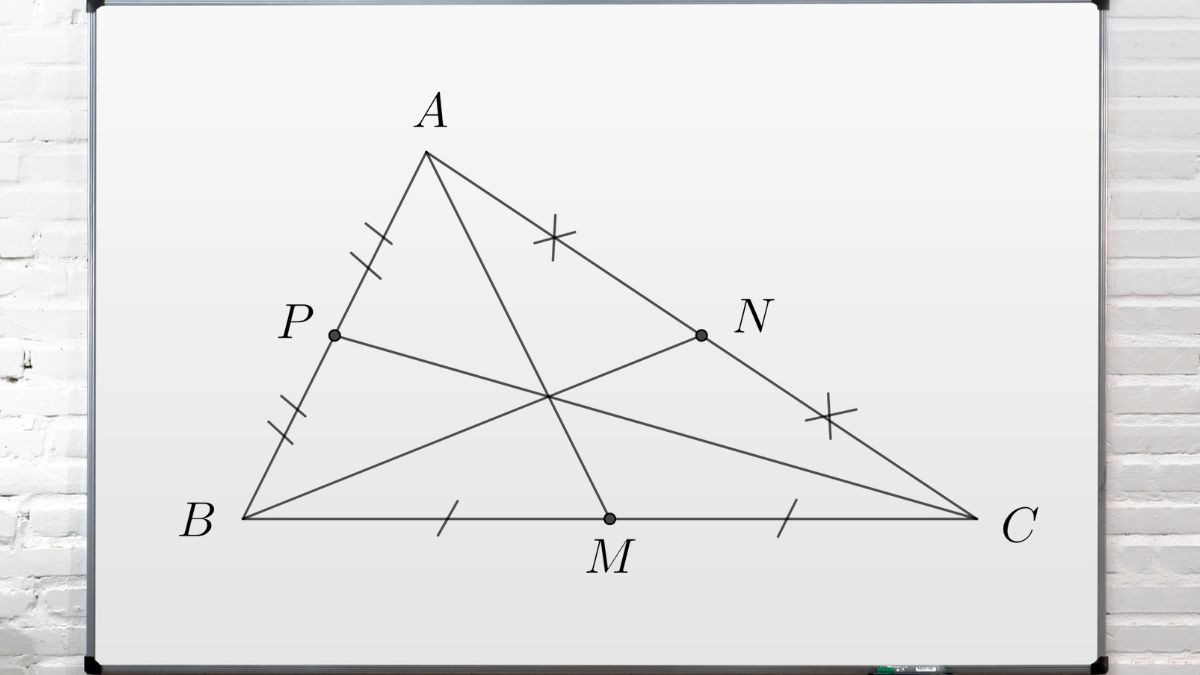
Alt: Giao điểm ba đường trung tuyến, thể hiện trọng tâm tam giác, một khái niệm quan trọng trong hình học.
Tính Chất Quan Trọng Của Đường Trung Tuyến Trong Tam Giác Cân
Tam giác cân là tam giác có hai cạnh bằng nhau. Đường trung tuyến xuất phát từ đỉnh cân (đỉnh tạo bởi hai cạnh bằng nhau) trong tam giác cân có những tính chất vô cùng đặc biệt:
- Đường trung tuyến đồng thời là đường cao: Đường trung tuyến này vuông góc với cạnh đáy.
- Đường trung tuyến đồng thời là đường phân giác: Đường trung tuyến này chia góc ở đỉnh cân thành hai góc bằng nhau.
- Đường trung tuyến đồng thời là đường trung trực: Đường trung tuyến này là đường trung trực của cạnh đáy.
Những tính chất này khiến đường trung tuyến từ đỉnh cân trở thành một yếu tố quan trọng để giải các bài toán liên quan đến tam giác cân.
Alt: Đường trung tuyến ứng với cạnh đáy tam giác cân, đồng thời thể hiện tính chất là đường cao và đường trung trực.
Ứng Dụng Của Đường Trung Tuyến Trong Giải Toán Tam Giác Cân
Hiểu rõ các tính chất của đường trung tuyến trong tam giác cân giúp chúng ta dễ dàng chứng minh các bài toán hình học, tính toán diện tích, chu vi và các yếu tố khác của tam giác. Ví dụ:
- Chứng minh hai tam giác bằng nhau: Nếu hai tam giác có một cạnh đáy bằng nhau và đường trung tuyến ứng với cạnh đáy đó cũng bằng nhau, thì hai tam giác đó bằng nhau.
- Tìm tâm đường tròn ngoại tiếp: Trong tam giác cân, giao điểm của đường trung tuyến (đồng thời là đường cao, đường trung trực) với đường trung trực của một cạnh bên chính là tâm đường tròn ngoại tiếp tam giác.
- Tính diện tích tam giác: Nếu biết độ dài cạnh đáy và đường trung tuyến ứng với cạnh đáy, ta có thể dễ dàng tính diện tích tam giác cân.
Alt: Tam giác đều với các đường trung tuyến, đường cao, đường phân giác và đường trung trực trùng nhau, thể hiện tính đối xứng cao.
Bài Tập Vận Dụng Về Tam Giác Cân Có Đường Trung Tuyến
Để củng cố kiến thức, hãy cùng xem xét một số bài tập sau:
Bài tập 1: Cho tam giác ABC cân tại A, đường trung tuyến AM. Biết AB = 10cm, BC = 12cm. Tính độ dài AM.
Hướng dẫn: Vì AM là đường trung tuyến của tam giác cân nên AM cũng là đường cao. Áp dụng định lý Pythagoras trong tam giác vuông ABM để tính AM.
Bài tập 2: Cho tam giác ABC cân tại A, đường trung tuyến AM. Chứng minh rằng tam giác ABM bằng tam giác ACM.
Hướng dẫn: Sử dụng định nghĩa tam giác cân và tính chất của đường trung tuyến để chứng minh các cạnh và góc tương ứng bằng nhau.
Bài tập 3: Cho tam giác ABC cân tại A, đường trung tuyến AM. Biết góc BAC = 50 độ. Tính góc ABM.
Hướng dẫn: Sử dụng tính chất đường trung tuyến đồng thời là đường phân giác để tính góc BAM, sau đó sử dụng tổng ba góc trong tam giác để tính góc ABM.
Alt: Sơ đồ minh họa mối quan hệ giữa trọng tâm và đường trung tuyến, tỷ lệ 2/3 và 1/3, kiến thức quan trọng trong hình học.
Kết Luận
Đường trung tuyến trong tam giác cân là một khái niệm quan trọng và hữu ích trong hình học. Việc nắm vững các tính chất và ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán hình học một cách dễ dàng và hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về “tam giác cân có đường trung tuyến”.