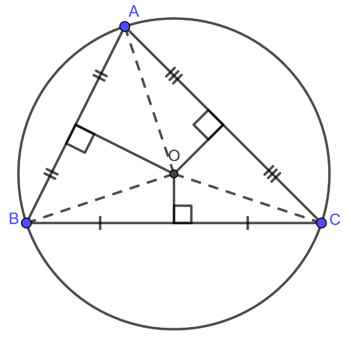
Đường tròn ngoại tiếp tam giác là một khái niệm quan trọng trong hình học. Để hiểu rõ về nó và giải quyết các bài toán liên quan, chúng ta cần nắm vững định nghĩa, tính chất và cách xác định tâm của đường tròn này.
1. Định Nghĩa Đường Tròn Ngoại Tiếp Tam Giác
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó. Tam giác đó được gọi là tam giác nội tiếp đường tròn.
Hình ảnh minh họa đường tròn ngoại tiếp tam giác ABC, thể hiện rõ tâm O và bán kính OA = OB = OC.
Vậy Tâm đường Tròn Ngoại Tiếp Tam Giác Là Giao điểm Của Ba đường Nào? Câu trả lời chính là: Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó.
2. Tính Chất Quan Trọng Của Đường Tròn Ngoại Tiếp Tam Giác
- Mỗi tam giác chỉ có duy nhất một đường tròn ngoại tiếp.
- Tâm của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác.
- Trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
- Trong tam giác đều, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp trùng nhau.
3. Các Kiến Thức Liên Quan Đến Đường Tròn Ngoại Tiếp Tam Giác
Để giải quyết các bài toán phức tạp hơn, chúng ta cần nắm vững các kiến thức sau:
3.1. Cách Vẽ Đường Tròn Ngoại Tiếp Tam Giác
Để vẽ đường tròn ngoại tiếp tam giác ABC, ta thực hiện các bước sau:
- Vẽ tam giác ABC.
- Dựng ba đường trung trực của tam giác.
- Xác định giao điểm I của ba đường trung trực, điểm này chính là tâm của đường tròn ngoại tiếp.
- Vẽ đường tròn tâm I bán kính IA (hoặc IB, IC).
3.2. Cách Xác Định Tọa Độ Tâm Đường Tròn Ngoại Tiếp Tam Giác
Có hai cách phổ biến để xác định tọa độ tâm đường tròn ngoại tiếp tam giác:
-
Cách 1: Gọi I(x; y) là tâm đường tròn ngoại tiếp tam giác ABC. Vì IA = IB = IC = R (bán kính), ta có thể lập hệ phương trình:
IA² = IB²
IA² = IC²Giải hệ phương trình này để tìm ra tọa độ (x; y) của tâm I.
-
Cách 2: Viết phương trình hai đường trung trực của hai cạnh của tam giác. Giao điểm của hai đường trung trực này chính là tâm của đường tròn ngoại tiếp.
Lưu ý: Với tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm cạnh huyền.
Hình ảnh phương trình tổng quát của đường tròn, áp dụng để tìm phương trình đường tròn ngoại tiếp tam giác.
3.3. Phương Trình Đường Tròn Ngoại Tiếp Tam Giác
Để viết phương trình đường tròn ngoại tiếp tam giác, ta thực hiện các bước sau:
- Giả sử phương trình đường tròn có dạng: x² + y² + 2ax + 2by + c = 0.
- Thay tọa độ ba đỉnh của tam giác vào phương trình trên, ta được một hệ ba phương trình bậc nhất ba ẩn a, b, c.
- Giải hệ phương trình này để tìm ra các giá trị a, b, c.
- Thay các giá trị a, b, c vừa tìm được vào phương trình ban đầu, ta được phương trình đường tròn ngoại tiếp tam giác.
3.4. Cách Tính Bán Kính Đường Tròn Ngoại Tiếp Tam Giác
Bán kính đường tròn ngoại tiếp tam giác có thể được tính bằng công thức:
R = (abc) / (4S)
Trong đó:
- a, b, c là độ dài ba cạnh của tam giác.
- S là diện tích của tam giác.
Công thức tính bán kính R của đường tròn ngoại tiếp tam giác ABC dựa trên độ dài các cạnh a, b, c và diện tích S của tam giác.
4. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy thử sức với một số bài tập sau:
- Bài 1: Cho tam giác ABC có tọa độ các đỉnh A(-1; 3), B(5; 1), C(-2; 3). Viết phương trình đường tròn ngoại tiếp tam giác ABC.
- Bài 2: Cho tam giác ABC có A(1; 3), B(-1; 1), C(2; 2). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
- Bài 3: Tam giác ABC đều có cạnh 8cm. Tính bán kính đường tròn ngoại tiếp tam giác.
- Bài 4: Tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính bán kính đường tròn ngoại tiếp tam giác.
Hy vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức về đường tròn ngoại tiếp tam giác và giúp bạn giải quyết các bài toán liên quan một cách dễ dàng.