Bạn đã bao giờ tự hỏi, tâm của đường tròn ngoại tiếp một tam giác được xác định như thế nào? Câu trả lời nằm ở một khái niệm hình học quan trọng: Tâm đường Tròn Ngoại Tiếp Tam Giác Là Giao điểm Của các đường trung trực của tam giác đó. Bài viết này sẽ đi sâu vào khám phá khái niệm này, cung cấp kiến thức đầy đủ và dễ hiểu nhất.
Đường tròn ngoại tiếp tam giác là một chủ đề quan trọng trong chương trình hình học phổ thông. Hiểu rõ về nó không chỉ giúp bạn giải quyết các bài tập liên quan mà còn mở ra cánh cửa khám phá những điều thú vị trong thế giới toán học.
1. Định Nghĩa và Khái Niệm Cơ Bản
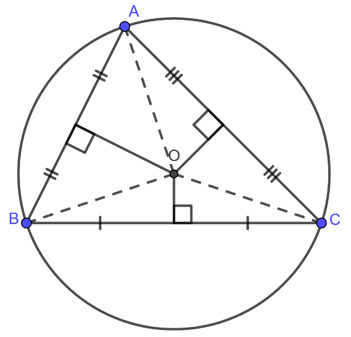
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó. Tâm của đường tròn ngoại tiếp, thường được ký hiệu là O, là điểm đặc biệt, đóng vai trò trung tâm trong nhiều bài toán hình học.
Hình ảnh minh họa đường tròn ngoại tiếp tam giác ABC, tâm O là giao điểm ba đường trung trực, thể hiện rõ tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực.
Vậy, tâm đường tròn ngoại tiếp tam giác là giao điểm của những đường nào? Đó chính là giao điểm của ba đường trung trực của tam giác. Đường trung trực của một cạnh là đường thẳng vuông góc với cạnh đó tại trung điểm của cạnh.
Khi nối tâm O với ba đỉnh của tam giác (OA, OB, OC), ta được ba đoạn thẳng có độ dài bằng nhau và bằng bán kính R của đường tròn ngoại tiếp. OA = OB = OC = R.
2. Tính Chất Quan Trọng Cần Nhớ
Đường tròn ngoại tiếp tam giác sở hữu những tính chất đặc biệt, giúp chúng ta giải quyết các bài toán một cách dễ dàng hơn:
- Mỗi tam giác chỉ có duy nhất một đường tròn ngoại tiếp.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác.
- Trong tam giác vuông, tâm đường tròn ngoại tiếp nằm ở trung điểm cạnh huyền.
- Trong tam giác đều, tâm đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp.
3. Cách Xác Định Tâm và Vẽ Đường Tròn Ngoại Tiếp
3.1. Xác định tâm đường tròn
Như đã đề cập, tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực. Do đó, để xác định tâm, ta thực hiện các bước sau:
- Vẽ tam giác ABC.
- Dựng hai (hoặc ba) đường trung trực của các cạnh tam giác.
- Giao điểm của các đường trung trực chính là tâm O của đường tròn ngoại tiếp.
3.2. Vẽ đường tròn ngoại tiếp
Sau khi xác định được tâm O, ta vẽ đường tròn đi qua ba đỉnh A, B, C của tam giác. Bán kính của đường tròn chính là khoảng cách từ tâm O đến một trong ba đỉnh (OA = OB = OC = R).
Hình ảnh minh họa các bước vẽ đường tròn ngoại tiếp tam giác, nhấn mạnh việc xác định đường trung trực và giao điểm của chúng.
4. Các Phương Pháp Tìm Tọa Độ Tâm Đường Tròn Ngoại Tiếp
Trong hình học tọa độ, việc tìm tọa độ tâm đường tròn ngoại tiếp là một bài toán thường gặp. Dưới đây là hai phương pháp phổ biến:
4.1. Phương pháp 1: Sử dụng tính chất khoảng cách
Gọi I(x; y) là tâm đường tròn ngoại tiếp tam giác ABC. Theo định nghĩa, ta có IA = IB = IC = R (R là bán kính). Do đó, tọa độ (x; y) của tâm I là nghiệm của hệ phương trình:
IA² = IB²
IA² = IC²
4.2. Phương pháp 2: Sử dụng phương trình đường trung trực
- Viết phương trình hai đường trung trực của hai cạnh bất kỳ của tam giác.
- Tìm giao điểm của hai đường trung trực đó. Giao điểm này chính là tâm của đường tròn ngoại tiếp.
Lưu ý: Đối với tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền.
5. Phương Trình Đường Tròn Ngoại Tiếp
Để viết phương trình đường tròn ngoại tiếp, ta thực hiện các bước sau:
- Giả sử phương trình đường tròn có dạng: x² + y² + 2ax + 2by + c = 0.
- Thay tọa độ ba đỉnh A, B, C của tam giác vào phương trình trên, ta được một hệ ba phương trình với ba ẩn a, b, c.
- Giải hệ phương trình để tìm a, b, c.
- Thay a, b, c vào phương trình ban đầu, ta được phương trình đường tròn ngoại tiếp.
Hình ảnh phương trình tổng quát của đường tròn và giải thích cách thay tọa độ điểm để tìm ra phương trình cụ thể.
6. Công Thức Tính Bán Kính Đường Tròn Ngoại Tiếp
Bán kính đường tròn ngoại tiếp tam giác có thể được tính bằng nhiều công thức khác nhau, tùy thuộc vào thông tin đã biết về tam giác. Một trong những công thức phổ biến nhất là:
R = (abc) / (4S)
Trong đó:
- a, b, c là độ dài ba cạnh của tam giác.
- S là diện tích của tam giác.
Hình ảnh công thức tính bán kính đường tròn ngoại tiếp tam giác, chú thích rõ ràng từng thành phần trong công thức.
7. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy cùng xem xét một số bài tập ví dụ:
Bài 1: Cho tam giác ABC với A(1; 2), B(3; -1), C(-2; 1). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
Bài 2: Cho tam giác đều ABC cạnh 6cm. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Bài 3: Chứng minh rằng trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm cạnh huyền.
Kết Luận
Hiểu rõ khái niệm tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực là chìa khóa để giải quyết nhiều bài toán hình học. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết và hữu ích. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài toán một cách thành thạo!