Hình bình hành là một dạng tứ giác đặc biệt và có nhiều ứng dụng trong toán học cũng như trong thực tế. Một trong những tính chất quan trọng của hình bình hành là tính đối xứng tâm. Bài viết này sẽ đi sâu vào khái niệm Tâm đối Xứng Của Hình Bình Hành, các tính chất liên quan và một số ví dụ minh họa.
Định nghĩa hình có tâm đối xứng
Một hình được gọi là có tâm đối xứng nếu tồn tại một điểm O sao cho khi quay hình đó 180 độ quanh điểm O, hình thu được trùng khớp hoàn toàn với hình ban đầu. Điểm O đó được gọi là tâm đối xứng của hình.
Tâm đối xứng của hình bình hành
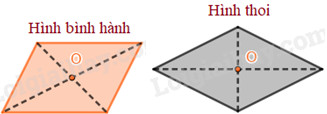
Hình bình hành là một hình có tâm đối xứng. Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Hình ảnh minh họa giao điểm hai đường chéo của hình bình hành, là tâm đối xứng của nó.
Chứng minh giao điểm hai đường chéo là tâm đối xứng
Cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Ta cần chứng minh O là tâm đối xứng của hình bình hành ABCD.
Để chứng minh, ta cần chứng minh rằng khi quay hình bình hành ABCD 180 độ quanh điểm O, ta thu được chính hình bình hành ABCD. Điều này tương đương với việc chứng minh điểm A biến thành điểm C, điểm B biến thành điểm D và ngược lại sau phép quay 180 độ quanh O.
- Vì O là giao điểm của AC và BD nên OA = OC và OB = OD.
- Khi quay điểm A quanh O 180 độ, vì OA = OC nên điểm A sẽ trùng với điểm C. Tương tự, điểm C sẽ trùng với điểm A.
- Khi quay điểm B quanh O 180 độ, vì OB = OD nên điểm B sẽ trùng với điểm D. Tương tự, điểm D sẽ trùng với điểm B.
Do đó, khi quay hình bình hành ABCD 180 độ quanh O, ta thu được chính hình bình hành ABCD. Vậy O là tâm đối xứng của hình bình hành ABCD.
Tính chất của tâm đối xứng trong hình bình hành
- Mọi đường thẳng đi qua tâm đối xứng của hình bình hành đều chia hình bình hành thành hai phần có diện tích bằng nhau.
- Tâm đối xứng là trung điểm của mọi đoạn thẳng nối hai điểm đối xứng nhau trên hình bình hành (ví dụ: trung điểm của AC, BD).
Ứng dụng của tâm đối xứng của hình bình hành
- Trong thiết kế: Tính đối xứng thường được sử dụng trong thiết kế kiến trúc, đồ họa và nhiều lĩnh vực khác để tạo ra sự cân bằng và hài hòa. Việc hiểu về tâm đối xứng của hình bình hành giúp các nhà thiết kế ứng dụng nó một cách hiệu quả.
- Trong toán học: Tâm đối xứng là một khái niệm quan trọng trong hình học, được sử dụng để giải quyết nhiều bài toán liên quan đến tính đối xứng và các tính chất của hình học.
- Trong thực tế: Nhiều vật thể trong thực tế có hình dạng gần giống hình bình hành và tính đối xứng của chúng có thể được sử dụng để phân tích và giải quyết các vấn đề liên quan.
Ví dụ minh họa
Xét một hình bình hành ABCD có tâm đối xứng O. Nếu biết tọa độ của các điểm A, B, C, ta có thể tìm tọa độ của điểm D bằng cách sử dụng tính chất tâm đối xứng: O là trung điểm của AC và BD.
Kết luận
Tâm đối xứng là một khái niệm quan trọng trong hình học và có nhiều ứng dụng thực tế. Việc hiểu rõ về tâm đối xứng của hình bình hành giúp chúng ta nắm vững các tính chất của hình bình hành và áp dụng chúng vào giải quyết các bài toán và các vấn đề trong cuộc sống.
Ảnh minh họa các vật thể quen thuộc có tâm đối xứng, nhấn mạnh tính ứng dụng của khái niệm này.