Bài viết này cung cấp kiến thức toàn diện về đường tròn ngoại tiếp tam giác, tập trung vào Tâm Của đường Tròn Ngoại Tiếp, giúp học sinh nắm vững khái niệm, tính chất và ứng dụng để giải quyết các bài toán liên quan.
1. Định Nghĩa Đường Tròn Ngoại Tiếp và Tâm Đường Tròn
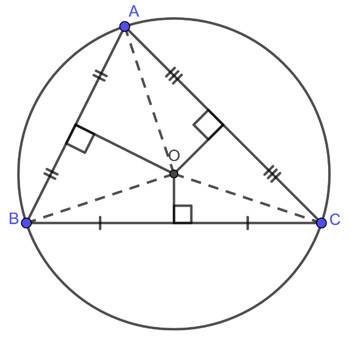
Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó. Tâm của đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác.
Một cách gọi khác của đường tròn ngoại tiếp tam giác là tam giác nội tiếp đường tròn (tam giác nằm trong đường tròn).
Hình ảnh minh họa đường tròn ngoại tiếp tam giác ABC, tâm O, và bán kính OA=OB=OC
Khi nối tâm O của đường tròn với ba đỉnh A, B, C, ta có OA = OB = OC, đây chính là bán kính của đường tròn ngoại tiếp tam giác ABC. Điều này rất quan trọng để giải quyết các bài toán.
2. Tính Chất Quan Trọng Của Đường Tròn Ngoại Tiếp
Các tính chất sau đây liên quan đến tâm của đường tròn ngoại tiếp là kiến thức then chốt:
- Mỗi tam giác chỉ có duy nhất một đường tròn ngoại tiếp.
- Giao điểm của ba đường trung trực của tam giác chính là tâm của đường tròn ngoại tiếp.
- Trong tam giác vuông, trung điểm cạnh huyền là tâm của đường tròn ngoại tiếp.
- Trong tam giác đều, tâm của đường tròn ngoại tiếp và tâm của đường tròn nội tiếp trùng nhau.
3. Kiến Thức Nâng Cao Về Đường Tròn Ngoại Tiếp và Cách Xác Định Tâm
Để giải quyết các bài toán phức tạp hơn, cần nắm vững các kiến thức nâng cao sau:
3.1. Cách Vẽ Đường Tròn Ngoại Tiếp Chính Xác
Nhắc lại: Tâm của đường tròn ngoại tiếp luôn là giao điểm của ba đường trung trực của tam giác.
Do đó, để vẽ đường tròn ngoại tiếp tam giác ABC, ta vẽ tam giác, sau đó vẽ các đường trung trực từ ba đỉnh để xác định tâm I. Cuối cùng, vẽ đường tròn tâm I với bán kính R = IA = IB = IC.
3.2. Các Phương Pháp Xác Định Tọa Độ Tâm Đường Tròn Ngoại Tiếp
Có hai cách chính để xác định tọa độ tâm của đường tròn ngoại tiếp:
Cách 1: Gọi I (x; y) là tâm của đường tròn ngoại tiếp. Theo tính chất, IA = IB = IC = R. Tọa độ (x; y) là nghiệm của hệ phương trình:
IA² = IB²
IA² = IC²
Cách 2: Viết phương trình hai đường trung trực của hai cạnh của tam giác. Giao điểm của hai đường trung trực này chính là tâm của đường tròn ngoại tiếp.
Lưu ý: Đối với tam giác vuông, tâm của đường tròn ngoại tiếp là trung điểm cạnh huyền. Cạnh huyền đồng thời là đường kính của đường tròn ngoại tiếp.
3.3. Phương Trình Đường Tròn Ngoại Tiếp Chi Tiết
Để viết phương trình đường tròn ngoại tiếp, thực hiện các bước sau:
- Bước 1: Thay tọa độ ba đỉnh của tam giác vào phương trình tổng quát của đường tròn: x² + y² + 2ax + 2by + c = 0. Do các đỉnh nằm trên đường tròn, tọa độ của chúng phải thỏa mãn phương trình.
- Bước 2: Giải hệ phương trình ba ẩn a, b, c để tìm ra các giá trị này.
- Bước 3: Thay a, b, c vừa tìm được vào phương trình tổng quát để được phương trình đường tròn ngoại tiếp.
Minh họa quá trình thiết lập phương trình đường tròn ngoại tiếp dựa trên tọa độ các đỉnh tam giác.
3.4. Công Thức Tính Bán Kính Đường Tròn Ngoại Tiếp
Cho tam giác ABC với các cạnh a, b, c. Bán kính R của đường tròn ngoại tiếp được tính theo công thức:
Công thức R = abc / 4S, trong đó S là diện tích tam giác.
4. Bài Tập Về Đường Tròn Ngoại Tiếp Tam Giác (Có Lời Giải Chi Tiết)
Dưới đây là một số bài tập ví dụ, giúp bạn luyện tập:
Bài 1: Cho tam giác ABC với A(-1;3), B(5;1), C(-2;3). Viết phương trình đường tròn ngoại tiếp tam giác ABC.
Bài 2: Cho tam giác ABC với A(1;3), B(-1;1), C(2;2). Tìm tọa độ tâm của đường tròn ngoại tiếp tam giác ABC.
Bài 3: Tam giác ABC đều có cạnh bằng 8cm. Xác định bán kính và tâm của đường tròn ngoại tiếp.
Bài 4: Tam giác ABC vuông tại A, AB=6 cm, AC=8 cm. Xác định tâm và bán kính đường tròn ngoại tiếp tam giác ABC. Tính bán kính đường tròn ngoại tiếp.
Bài 5: Cho tam giác MNP nhọn nội tiếp đường tròn (O; R). Ba đường cao MF, NE, PD cắt nhau tại H. Chứng minh tứ giác NDEP nội tiếp được trong một đường tròn.
Bài viết này đã cung cấp đầy đủ kiến thức về đường tròn ngoại tiếp tam giác, đặc biệt tập trung vào tâm của đường tròn ngoại tiếp. Hy vọng bạn sẽ áp dụng thành công vào giải toán.