Định lý Talet là một công cụ mạnh mẽ trong hình học, đặc biệt hữu ích khi giải các bài toán liên quan đến hình thang và tam giác. Bài viết này sẽ tập trung vào định lý Talet Trong Hình Thang, cung cấp kiến thức sâu rộng và các bài tập áp dụng.
Định Nghĩa Tỉ Số của Hai Đoạn Thẳng
Tỉ số của hai đoạn thẳng là tỉ lệ độ dài của chúng khi được đo bằng cùng một đơn vị. Tỉ số của hai đoạn thẳng AB và CD được ký hiệu là (dfrac{AB}{CD}).
Hai đoạn thẳng AB và CD được gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu chúng thỏa mãn tỉ lệ thức:
Alt: Tỉ lệ thức thể hiện mối quan hệ tỉ lệ giữa các đoạn thẳng AB, CD, A’B’ và C’D’
Định Lý Talet Trong Tam Giác
Định Lý Talet Thuận
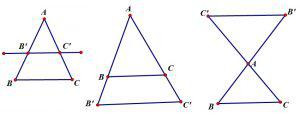
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại, nó sẽ tạo ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Ví dụ, xét tam giác ABC, nếu B’C’ // BC thì:
Alt: Hình ảnh minh họa định lý Talet thuận trong tam giác ABC, với đường thẳng B’C’ song song với BC
Định Lý Talet Đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và tạo ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ, thì đường thẳng đó song song với cạnh còn lại của tam giác.
Cho tam giác ABC, nếu một trong các điều kiện sau đúng:
Alt: Các tỉ lệ thức thể hiện định lý Talet đảo trong tam giác ABC, chứng minh B’C’ song song BC
thì suy ra B’C’ // BC.
Hệ Quả của Định Lý Talet
Nếu một đường thẳng cắt hai cạnh (hoặc phần kéo dài của hai cạnh) của một tam giác và song song với cạnh còn lại, nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác ban đầu.
Alt: Minh họa hệ quả định lý Talet, tam giác AB’C’ có các cạnh tỉ lệ với tam giác ABC
(Rightarrow frac{AB’}{AB}=frac{AC’}{AC}=frac{B’C’}{BC})
Định Lý Talet Trong Hình Thang
Định lý Talet mở rộng cho hình thang nói rằng nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên, nó sẽ tạo ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
Alt: Hình thang ABCD với EF song song AB và CD, minh họa định lý Talet
Cho hình thang ABCD, với E thuộc AD và F thuộc BC. Nếu EF // AB // CD, thì ta có: (frac{AE}{DE}=frac{BF}{CF}).
Ngược lại, nếu (frac{AE}{DE}=frac{BF}{CF}) thì EF // AB // CD.
Ví dụ: Cho hình thang ABCD (AB // CD), và MN song song với AB và CD, với M thuộc AD và N thuộc BC. Biết AM = 3, AD = 2, BC = 6. Tính BN.
Giải: Vì hình thang ABCD có AB // CD // MN, theo định lý Talet trong hình thang ABCD, ta có:
(Rightarrowfrac{AM}{AD}=frac{BN}{BC}Rightarrow BN=frac{AM.BC}{AD}=frac{3.6}{2}=9)
Bài Tập Luyện Tập
Câu hỏi trắc nghiệm
Bài 1. Tính tỉ số của các cặp đoạn thẳng sau:
a) AB = 6 cm; CD = 10 cm.
b) AB = 2 dm; MN = 4 cm.
c) MN = 12 cm; PQ = 2 dm.
Bài 2: Tìm giá trị của x trên hình vẽ:
Alt: Hình vẽ tam giác và đường thẳng song song, yêu cầu tìm giá trị x
A. x = 3
B. x = 2,5
C. x = 1
D. x = 3,5
Bài 3: Cho hình vẽ, DE // BC, AE = 12, DB = 18, CA = 36. Tính độ dài AB:
Alt: Hình vẽ tam giác với các đoạn thẳng đã biết, yêu cầu tính AB
A. 30
B. 36
C. 25
D. 27
Câu hỏi tự luận
Bài tập 1: Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với A qua B. Trên tia đối của tia HA lấy E sao cho HE = 2HA. Gọi I là hình chiếu của D trên HE. Tính AB, AC, HC biết AH = 4cm, HB = 3cm.
Bài tập 2: Cho hình bình hành ABCD. Gọi E, F, G lần lượt là trung điểm của AB, BC, CD. Chứng minh DE và BG chia AC thành 3 đoạn bằng nhau bằng cách sử dụng định lý Talet.
Bài tập 3: Cho hình thang ABCD (CD là đáy nhỏ). Từ D kẻ DK // BC (K thuộc AB), DK cắt AC tại M. Vẽ CF // AD (F thuộc AB). Qua F kẻ FP // AC (P thuộc BC). Chứng minh MP // AB.
Bài tập 4: Cho tam giác ABC, M là trung điểm của AB. Từ M kẻ đường thẳng song song với BC cắt AC tại N. Chứng minh rằng N là trung điểm của AC.
Bài tập 5: Cho tam giác ABC, các trung tuyến AD, BE, CF cắt nhau tại G. Tính AE/AC bằng cách áp dụng định lý Talet.
Bài tập 6: Trên cạnh BC của hình vuông ABCD, lấy điểm E sao cho BE = 1/3BC. Trên tia đối của tia CD, lấy điểm F sao cho CF = 1/2BC. Gọi M là giao điểm của AE và BF. Chứng minh AM vuông góc với CM.
Bài tập 7: Hình thang ABCD (AB//CD, ABBài tập 8: Hình thang ABCD (AB//CD, ABBài tập 9: Hình thang ABCD (AB//CD, ABa) Chứng minh MN // AB.
b) Tính MN.
Bài tập 10: Hình thang ABCD (AB//CD,ABBài tập 11: Cho hình thang ABCD (AB//CD,ABa) Chứng minh: IK // AB.
b) Đường thẳng IK cắt AD, BC lần lượt tại E và F. Chứng minh: EI = IK = KF.
Bài tập 12: Cho hình thang ABCD có BC // AD. Trên AC kéo dài lấy điểm P bất kỳ. Đường thẳng qua P và trung điểm của BC cắt AB tại M và đường thẳng qua P và trung điểm của AD cắt CD tại N. Chứng minh rằng MN // AD.
Bài tập 13: Tứ giác ABCD có M, N lần lượt là trung điểm của các đường chéo AC và BD. Gọi G là trọng tâm tam giác ABC. Nối GC cắt MN tại O. Chứng minh rằng OC = 3 OG.
Bài tập 14. Tìm độ dài x cho hình vẽ sau biết MN// BC.
Bài tập 15. Cho các đoạn thẳng AB = 4 cm; CD = 8cm; MN = 20cm; PQ = x cm. Tìm x để AB và CD tỉ lệ với MN và PQ.
Hy vọng qua bài viết này, bạn đã nắm vững định lý Talet trong hình thang và có thể áp dụng nó để giải quyết các bài toán hình học một cách hiệu quả.