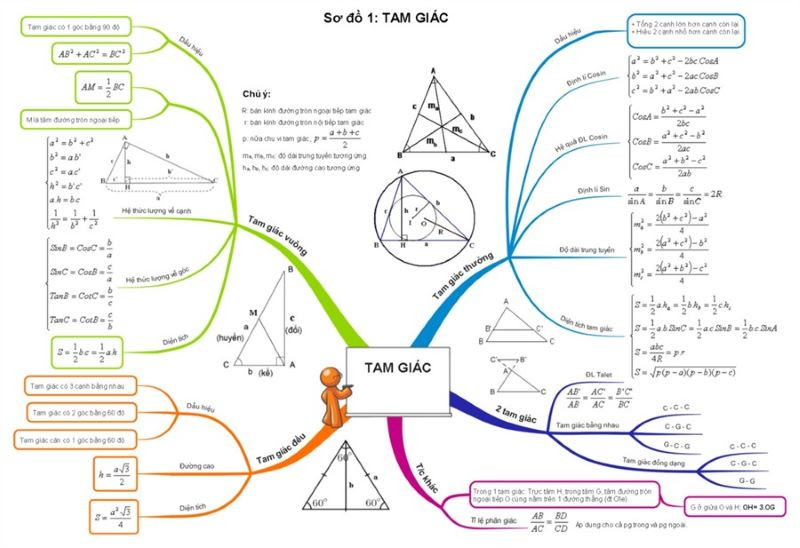
Sơ đồ Tư Duy Hệ Thức Lượng Trong Tam Giác là công cụ đắc lực giúp học sinh lớp 9 nắm vững kiến thức, giải quyết bài tập hiệu quả và tự tin chinh phục các kỳ thi quan trọng. Bài viết này sẽ cung cấp cái nhìn tổng quan và chi tiết về cách sử dụng sơ đồ tư duy để làm chủ hệ thức lượng trong tam giác, giúp bạn học tập một cách thông minh và khoa học.
Hệ Thức Lượng Trong Tam Giác: Nền Tảng Quan Trọng
Hệ thức lượng trong tam giác là một chủ đề quan trọng trong chương trình toán lớp 9, đặc biệt là hình học. Nắm vững các hệ thức này giúp học sinh giải quyết các bài toán liên quan đến tính độ dài cạnh, góc, diện tích của tam giác, đặc biệt là tam giác vuông. Việc hiểu rõ và vận dụng linh hoạt các công thức này sẽ là nền tảng vững chắc cho các kỳ thi và các lớp học cao hơn.
Vì Sao Nên Sử Dụng Sơ Đồ Tư Duy?
Sơ đồ tư duy (mind map) là một công cụ trực quan giúp tổ chức thông tin, kết nối các khái niệm và ghi nhớ kiến thức một cách hiệu quả. Khi áp dụng sơ đồ tư duy vào việc học hệ thức lượng trong tam giác, bạn sẽ thấy những lợi ích sau:
- Hệ thống hóa kiến thức: Sơ đồ tư duy giúp bạn sắp xếp các công thức, định lý, khái niệm một cách logic và có hệ thống, dễ dàng tra cứu và ôn tập.
- Tăng cường khả năng ghi nhớ: Hình ảnh, màu sắc và sự liên kết giữa các nhánh trong sơ đồ tư duy giúp tăng cường khả năng ghi nhớ kiến thức một cách trực quan và lâu dài.
- Phát triển tư duy logic: Việc tạo sơ đồ tư duy đòi hỏi bạn phải phân tích, tổng hợp và liên kết các kiến thức, từ đó phát triển tư duy logic và khả năng giải quyết vấn đề.
- Tiết kiệm thời gian học tập: Thay vì học thuộc lòng một cách máy móc, sơ đồ tư duy giúp bạn nắm bắt kiến thức một cách nhanh chóng và hiệu quả, tiết kiệm thời gian học tập.
Xây Dựng Sơ Đồ Tư Duy Hệ Thức Lượng Trong Tam Giác
Để xây dựng một sơ đồ tư duy hiệu quả cho hệ thức lượng trong tam giác, bạn có thể làm theo các bước sau:
-
Xác định chủ đề chính: Ghi chủ đề chính “Hệ Thức Lượng Trong Tam Giác” ở trung tâm sơ đồ.
-
Phân loại các nhánh chính: Chia sơ đồ thành các nhánh chính, mỗi nhánh đại diện cho một loại tam giác hoặc một nhóm công thức quan trọng. Ví dụ:
- Tam giác vuông
- Tam giác thường
- Hệ thức về cạnh và góc
- Hệ thức về diện tích
-
Phát triển các nhánh con: Từ mỗi nhánh chính, phát triển các nhánh con chứa các công thức, định lý, ví dụ minh họa cụ thể. Ví dụ, trong nhánh “Tam giác vuông”, bạn có thể có các nhánh con sau:
- Định lý Pytago
- Các hệ thức lượng về cạnh và góc (sin, cos, tan, cot)
- Các hệ thức liên quan đến đường cao, trung tuyến
-
Sử dụng hình ảnh, màu sắc: Sử dụng hình ảnh, biểu tượng và màu sắc để làm cho sơ đồ tư duy trở nên sinh động và dễ nhớ hơn.
-
Liên kết các nhánh: Sử dụng mũi tên hoặc đường kẻ để liên kết các nhánh có liên quan với nhau, thể hiện mối quan hệ giữa các khái niệm.
Các Nội Dung Chính Trong Sơ Đồ Tư Duy Hệ Thức Lượng
Dưới đây là một số nội dung chính nên có trong sơ đồ tư duy hệ thức lượng trong tam giác:
1. Tam Giác Vuông
- Định lý Pytago: $a^2 + b^2 = c^2$ (với a, b là cạnh góc vuông, c là cạnh huyền)
- Các hệ thức lượng về cạnh và góc:
- sin α = đối / huyền
- cos α = kề / huyền
- tan α = đối / kề
- cot α = kề / đối
- Các hệ thức liên quan đến đường cao: $h^2 = b’c’$, $ab = ch$, $frac{1}{h^2} = frac{1}{b^2} + frac{1}{c^2}$ (với h là đường cao ứng với cạnh huyền, b’, c’ là hình chiếu của cạnh góc vuông lên cạnh huyền)
2. Tam Giác Thường
- Định lý Cosin: $a^2 = b^2 + c^2 – 2bc cdot cosA$
- Định lý Sin: $frac{a}{sinA} = frac{b}{sinB} = frac{c}{sinC} = 2R$ (với R là bán kính đường tròn ngoại tiếp)
3. Hệ Thức Về Diện Tích
- $S = frac{1}{2} cdot a cdot h_a$ (với $h_a$ là chiều cao ứng với cạnh a)
- $S = frac{1}{2} cdot ab cdot sinC$
- $S = sqrt{p(p-a)(p-b)(p-c)}$ (công thức Heron, với $p = frac{a+b+c}{2}$ là nửa chu vi)
- $S = frac{abc}{4R}$
- $S = p cdot r$ (với r là bán kính đường tròn nội tiếp)
4. Ứng Dụng
- Giải các bài toán tính độ dài cạnh, góc, diện tích tam giác
- Chứng minh các đẳng thức hình học
- Giải các bài toán thực tế liên quan đến tam giác
Ví Dụ Về Sơ Đồ Tư Duy Hệ Thức Lượng Trong Tam Giác
Bạn có thể tham khảo các sơ đồ tư duy mẫu trên internet hoặc tự tạo sơ đồ tư duy của riêng mình. Điều quan trọng là sơ đồ đó phải phù hợp với cách học và cách ghi nhớ của bạn.
Lời Khuyên Khi Sử Dụng Sơ Đồ Tư Duy
- Thường xuyên ôn tập: Sau khi tạo sơ đồ tư duy, hãy thường xuyên ôn tập để củng cố kiến thức.
- Áp dụng vào giải bài tập: Sử dụng sơ đồ tư duy để phân tích và giải các bài tập hệ thức lượng trong tam giác.
- Tự tạo sơ đồ tư duy: Tự tạo sơ đồ tư duy của riêng bạn để tăng cường khả năng ghi nhớ và hiểu sâu kiến thức.
- Sử dụng phần mềm hỗ trợ: Có nhiều phần mềm hỗ trợ tạo sơ đồ tư duy trực tuyến, giúp bạn tạo sơ đồ một cách dễ dàng và chuyên nghiệp.
Kết Luận
Sơ đồ tư duy hệ thức lượng trong tam giác là một công cụ học tập mạnh mẽ, giúp bạn nắm vững kiến thức, phát triển tư duy logic và đạt kết quả cao trong môn toán. Hãy bắt đầu tạo sơ đồ tư duy của riêng bạn ngay hôm nay và khám phá những lợi ích tuyệt vời mà nó mang lại!