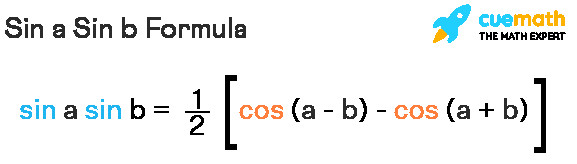Sina Sinb là một công thức quan trọng trong lượng giác, được sử dụng để đơn giản hóa nhiều bài toán. Công thức này có thể được chứng minh bằng cách sử dụng công thức cộng và trừ của hàm cosin. Nó được dùng để tìm tích của hàm sin cho các góc a và b. Kết quả của công thức sina sinb được biểu diễn là (1/2)[cos(a – b) – cos(a + b)].
Chúng ta sẽ cùng tìm hiểu chi tiết về công thức sin a sin b, cách chứng minh và ứng dụng của nó trong giải quyết các bài toán toán học khác nhau.
Sina Sinb trong Lượng Giác Là Gì?
Sina Sinb là một đẳng thức lượng giác cho hai góc khác nhau mà tổng và hiệu của chúng đã biết. Nó được áp dụng khi hai góc a và b đã biết, hoặc khi tổng và hiệu của các góc đã biết. Công thức này có thể được chứng minh bằng cách sử dụng các đẳng thức tổng và hiệu của hàm cosin: cos (a + b) và cos (a – b). Đây là một số đẳng thức lượng giác quan trọng.
Công thức Sina Sinb được sử dụng để xác định tích của hàm sin cho các góc a và b riêng biệt. Công thức sina sinb bằng một nửa hiệu của cosin của hiệu và tổng của các góc a và b, tức là, sina sinb = (1/2)[cos(a – b) – cos(a + b)].
Công Thức Sina Sinb
Công thức tích thành tổng của sina sinb trong lượng giác cho các góc a và b được cho như sau: sina sinb = (1/2)[cos(a – b) – cos(a + b)]. Trong đó, a và b là các góc, và (a + b) và (a – b) là các góc hợp của chúng. Công thức Sina Sinb được sử dụng khi các góc a và b đã cho hoặc tổng và hiệu của chúng đã cho.
Chứng Minh Công Thức Sina Sinb
Bây giờ, sau khi đã biết công thức sina sinb, chúng ta sẽ chứng minh công thức này bằng cách sử dụng các đẳng thức tổng và hiệu của hàm cosin. Các đẳng thức lượng giác mà chúng ta sẽ sử dụng để chứng minh công thức sin a sin b là:
- cos (a + b) = cos a cos b – sin a sin b — (1)
- cos (a – b) = cos a cos b + sin a sin b — (2)
Trừ phương trình (1) từ (2), ta có:
cos (a – b) – cos (a + b) = (cos a cos b + sin a sin b) – (cos a cos b – sin a sin b)
⇒ cos (a – b) – cos (a + b) = cos a cos b + sin a sin b – cos a cos b + sin a sin b
⇒ cos (a – b) – cos (a + b) = cos a cos b – cos a cos b + sin a sin b + sin a sin b
⇒ cos (a – b) – cos (a + b) = sin a sin b + sin a sin b [cos a cos b bị triệt tiêu do dấu trái ngược]
⇒ cos (a – b) – cos (a + b) = 2 sin a sin b
⇒ sin a sin b = (1/2)[cos (a – b) – cos (a + b)]
Do đó, công thức sina sinb đã được chứng minh.
Vậy, sina sinb = (1/2)[cos(a – b) – cos(a + b)]
Cách Áp Dụng Công Thức Sina Sinb?
Tiếp theo, chúng ta sẽ tìm hiểu cách áp dụng công thức sina sinb trong giải quyết các bài toán khác nhau sau khi đã chứng minh công thức. Đẳng thức sin a sin b có thể được sử dụng để giải các bài toán lượng giác đơn giản và các bài toán tích phân phức tạp. Hãy xem xét một vài ví dụ để hiểu rõ hơn về khái niệm này và làm theo các bước dưới đây để học cách áp dụng đẳng thức sin a sin b:
Ví dụ 1: Biểu diễn sin x sin 7x dưới dạng hiệu của hàm cosin bằng công thức sina sinb.
Bước 1: Chúng ta biết rằng sin a sin b = (1/2)[cos(a – b) – cos(a + b)].
Xác định a và b trong biểu thức đã cho. Ở đây a = x, b = 7x. Sử dụng công thức trên, chúng ta sẽ chuyển sang bước thứ hai.
Bước 2: Thay thế các giá trị của a và b vào công thức.
sin x sin 7x = (1/2)[cos (x – 7x) – cos (x + 7x)]
⇒ sin x sin 7x = (1/2)[cos (-6x) – cos (8x)]
⇒ sin x sin 7x = (1/2) cos (6x) – (1/2) cos (8x) [Vì cos(-a) = cos a]
Do đó, sin x sin 7x có thể được biểu diễn dưới dạng (1/2) cos (6x) – (1/2) cos (8x) dưới dạng hiệu của hàm cosin.
Ví dụ 2: Giải tích phân ∫ sin 2x sin 5x dx.
Để giải tích phân ∫ sin 2x sin 5x dx, chúng ta sẽ sử dụng công thức sin a sin b.
Bước 1: Chúng ta biết rằng sin a sin b = (1/2)[cos(a – b) – cos(a + b)]
Xác định a và b trong biểu thức đã cho. Ở đây a = 2x, b = 5x. Sử dụng công thức trên, ta có:
Bước 2: Thay thế các giá trị của a và b vào công thức và giải tích phân.
sin 2x sin 5x = (1/2)[cos (2x – 5x) – cos (2x + 5x)]
⇒ sin 2x sin 5x = (1/2)[cos (-3x) – cos (7x)]
⇒ sin 2x sin 5x = (1/2)cos (3x) – (1/2)cos (7x) [Vì cos(-a) = cos a]
Bước 3: Bây giờ, thay thế sin 2x sin 5x = (1/2)cos (3x) – (1/2)cos (7x) vào tích phân ∫ sin 2x sin 5x dx. Chúng ta sẽ sử dụng công thức tích phân của hàm cosin ∫ cos x = sin x + C
∫ sin 2x sin 5x dx = ∫ [(1/2)cos (3x) – (1/2)cos (7x)] dx
⇒ ∫ sin 2x sin 5x dx = (1/2) ∫ cos (3x) dx – (1/2) ∫ cos (7x) dx
⇒ ∫ sin 2x sin 5x dx = (1/2) [sin (3x)]/3 – (1/2) [sin (7x)]/7 + C
⇒ ∫ sin 2x sin 5x dx = (1/6) sin (3x) – (1/14) sin (7x) + C
Do đó, tích phân ∫ sin 2x sin 5x dx = (1/6) sin (3x) – (1/14) sin (7x) + C sử dụng công thức sin a sin b.
Lưu ý quan trọng về công thức sina sinb
- sin a sin b được áp dụng khi hai góc a và b đã biết hoặc khi tổng và hiệu của các góc đã biết.
- sin a sin b = (1/2)[cos(a – b) – cos(a + b)]
- Nó có thể được chứng minh bằng cách sử dụng các đẳng thức tổng và hiệu của hàm cosin
Ví Dụ Về Sina Sinb
Ví dụ 1: Giải tích phân ∫ sin 9x sin 3x dx bằng cách sử dụng đẳng thức sina sinb.
Giải: Ta biết rằng sina sinb = (1/2)[cos (a – b) – cos (a + b)]
Xác định a và b trong biểu thức đã cho. Ở đây a = 9x, b = 3x. Sử dụng công thức trên, ta có:
sin 9x sin 3x = (1/2)[cos (9x – 3x) – cos (9x + 3x)]
⇒ sin 9x sin 3x = (1/2)[cos (6x) – cos (12x)]
⇒ sin 9x sin 3x = (1/2)cos (6x) – (1/2)cos (12x)
Bây giờ, thay thế sin 9x sin 3x = (1/2)cos (6x) – (1/2)cos (12x) vào tích phân ∫ sin 9x sin 3x dx. Chúng ta sẽ sử dụng công thức tích phân của hàm cosin ∫ cos x dx = sin x + C
∫ sin 9x sin 3x dx = ∫ [(1/2)cos (6x) – (1/2)cos (12x)] dx
⇒ ∫ sin 9x sin 3x dx = (1/2) ∫ cos (6x) dx – (1/2) ∫ cos (12x) dx
⇒ ∫ sin 9x sin 3x dx = (1/2) [sin (6x)]/6 – (1/2) [sin (12x)]/12 + C
⇒ ∫ sin 9x sin 3x dx = (1/12) sin (6x) – (1/24) sin (12x) + C
Đáp án: ∫ sin 9x sin 3x dx = (1/12) sin (6x) – (1/24) sin (12x) + C
Ví dụ 2: Xác định giá trị của sin 15° sin 45° bằng công thức sin a sin b.
Giải: Ta biết rằng sin a sin b = (1/2)[cos (a – b) – cos (a + b)]
Xác định a và b trong biểu thức đã cho. Ở đây a = 15°, b = 45°. Sử dụng công thức trên, ta có:
sin 15° sin 45° = (1/2)[cos (15° – 45°) – cos (15° + 45°)]
⇒ sin 15° sin 45° = (1/2)[cos (- 30°) – cos (60°)]
⇒ sin 15° sin 45° = (1/2)[cos (30°) – cos (60°)] [Vì cos(-a) = cos a]
⇒ sin 15° sin 45° = (1/2)[√3/2 – 1/2]
⇒ sin 15° sin 45° = (√3 – 1)/4
Đáp án: sin 15° sin 45° = (√3 – 1)/4
Các Câu Hỏi Thường Gặp Về Sina Sinb
Công thức Sina Sinb trong lượng giác là gì?
Sina Sinb là một công thức quan trọng trong lượng giác được sử dụng để đơn giản hóa các bài toán lượng giác. Công thức sin a sin b là sin a sin b = (1/2)[cos(a – b) – cos(a + b)].
Công thức của 2 Sina sinb là gì?
Chúng ta biết rằng sina sinb = (1/2)[cos(a – b) – cos(a + b)] ⇒ 2 sin a sin b = cos(a – b) – cos(a + b). Do đó, công thức của 2 sin a sin b là cos(a – b) – cos(a + b).
Làm thế nào để chứng minh đẳng thức sina sinb?
Các đẳng thức lượng giác được sử dụng để chứng minh công thức sina sinb là:
- cos (a + b) = cos a cos b – sin a sin b
- cos (a – b) = cos a cos b + sin a sin b
Trừ hai phương trình trên và đơn giản hóa để chứng minh đẳng thức sin a sin b.
Khai triển của Sina Sinb trong lượng giác là gì?
Công thức khai triển sina sinb trong lượng giác cho các góc a và b được cho như sau: sin a sin b = (1/2)[cos(a – b) – cos(a + b)]. Trong đó, a và b là các góc, và (a + b) và (a – b) là các góc hợp của chúng.
Làm thế nào để áp dụng công thức Sina Sinb?
Đẳng thức sina sinb có thể được sử dụng để giải các bài toán lượng giác đơn giản và các bài toán tích phân phức tạp. Công thức cho sin a sin b có thể được áp dụng theo cos (a – b) và cos (a + b) để giải quyết các bài toán khác nhau.
Làm thế nào để sử dụng đẳng thức sina sinb trong lượng giác?
Để sử dụng công thức sin a sin b, so sánh biểu thức đã cho với công thức sin a sin b = (1/2)[cos(a – b) – cos(a + b)] và thay thế các giá trị tương ứng của các góc a và b để giải quyết vấn đề.