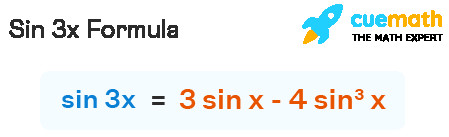Trong lượng giác, Sin3x = là một công thức quan trọng, biểu diễn giá trị của hàm sin cho góc gấp ba. Bài viết này sẽ đi sâu vào công thức sin3x, cách chứng minh, đồ thị và các ứng dụng của nó, giúp bạn nắm vững kiến thức và giải quyết các bài toán liên quan một cách hiệu quả.
Công Thức Sin3x
Công thức lượng giác cho sin3x được biểu diễn như sau:
sin3x = 3sinx – 4sin³x
Công thức này cho phép chúng ta tính giá trị sin của góc 3x dựa trên giá trị sin của góc x.
Đồ Thị Hàm Số Sin3x
Đồ thị của hàm số sin3x có dạng tương tự như đồ thị của hàm số sinx, nhưng có chu kỳ ngắn hơn. Chu kỳ của sinx là 2π, trong khi chu kỳ của sin3x là 2π/3. Điều này có nghĩa là đồ thị sin3x sẽ “nén” lại so với đồ thị sinx.
Để vẽ đồ thị sin3x, chúng ta có thể xác định một số điểm đặc biệt:
- Khi x = 0, sin3x = 0
- Khi x = π/6, sin3x = 1
- Khi x = π/2, sin3x = -1
- Khi x = 5π/6, sin3x = 1
- Khi x = π, sin3x = 0
Chứng Minh Công Thức Sin3x
Để chứng minh công thức sin3x, ta sử dụng công thức cộng góc lượng giác:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
Áp dụng công thức này cho sin3x = sin(2x + x), ta có:
sin3x = sin(2x)cos(x) + cos(2x)sin(x)
Sử dụng các công thức sin2x = 2sinxcosx và cos2x = 1 – 2sin²x, ta được:
sin3x = (2sinxcosx)cosx + (1 – 2sin²x)sinx
= 2sinxcos²x + sinx – 2sin³x
= 2sinx(1 – sin²x) + sinx – 2sin³x
= 2sinx – 2sin³x + sinx – 2sin³x
= 3sinx – 4sin³x
Vậy, sin3x = 3sinx – 4sin³x (đpcm)
Công Thức Sin³x (Sin Lập Phương x)
Từ công thức sin3x, ta có thể suy ra công thức cho sin³x:
sin3x = 3sinx – 4sin³x
=> 4sin³x = 3sinx – sin3x
=> sin³x = (3sinx – sin3x) / 4
Công thức này hữu ích trong việc đơn giản hóa các biểu thức lượng giác và tính tích phân.
Ví Dụ Minh Họa
Ví dụ 1: Tính giá trị của sin(3π/2) sử dụng công thức sin3x.
Giải:
Đặt 3x = 3π/2 => x = π/2
sin(3π/2) = 3sin(π/2) – 4sin³(π/2)
= 3(1) – 4(1)³
= 3 – 4 = -1
Ví dụ 2: Chứng minh rằng sin(π) = 0 sử dụng công thức sin3x.
Giải:
Đặt 3x = π => x = π/3
sin(π) = 3sin(π/3) – 4sin³(π/3)
= 3(√3/2) – 4(√3/2)³
= 3√3/2 – 4(3√3/8)
= 3√3/2 – 3√3/2 = 0
Ứng Dụng của Sin3x
Công thức sin3x có nhiều ứng dụng trong toán học, vật lý và kỹ thuật, bao gồm:
- Giải các phương trình lượng giác.
- Đơn giản hóa các biểu thức lượng giác phức tạp.
- Tính tích phân các hàm lượng giác.
- Phân tích dao động và sóng.
Công thức sin3x là một công cụ hữu ích trong nhiều lĩnh vực khoa học và kỹ thuật.
Các Câu Hỏi Thường Gặp (FAQ)
1. sin3x có bằng 3sinx không?
Không, sin3x khác với 3sinx. sin3x là giá trị của hàm sin tại góc 3x, trong khi 3sinx là ba lần giá trị của hàm sin tại góc x.
2. Công thức đạo hàm của sin3x là gì?
Đạo hàm của sin3x là 3cos3x.
3. Công thức tích phân của sin3x là gì?
Tích phân của sin3x là (-1/3)cos3x + C, trong đó C là hằng số tích phân.
4. Làm thế nào để vẽ đồ thị sin3x?
Bạn có thể vẽ đồ thị sin3x bằng cách xác định một số điểm đặc biệt và nối chúng lại. Đồ thị sin3x có chu kỳ là 2π/3.
5. sin³x có nghĩa là gì?
sin³x là sin lập phương của x, tức là (sinx)³. Nó khác với sin3x.
Hy vọng bài viết này đã cung cấp cho bạn cái nhìn toàn diện về công thức sin3x =, từ công thức, chứng minh, đồ thị đến các ứng dụng thực tế. Chúc bạn học tốt!