Công thức sin2x là một trong những công thức lượng giác quan trọng, được sử dụng rộng rãi trong giải toán và các ứng dụng thực tế. Bài viết này sẽ cung cấp đầy đủ kiến thức về sin2x, từ công thức cơ bản đến các ví dụ minh họa và ứng dụng, giúp bạn nắm vững và sử dụng hiệu quả công thức này.
A. Công Thức Sin2x Cơ Bản
Công thức sin2x được định nghĩa như sau:
sin 2x = 2 sin x . cos x
Đây là công thức nhân đôi của hàm sin, cho phép biểu diễn sin của góc gấp đôi thông qua sin và cos của góc ban đầu.
Ví dụ 1: Biến đổi biểu thức A = 1 + sin 2x thành tích.
Hướng dẫn giải:
A = 1 + sin 2x
A = sin² x + cos² x + 2 . sin x . cos x (Sử dụng sin²x + cos²x = 1)
A = (sin x + cos x)²
A = (sin x + cos x) . (sin x + cos x)
Ví dụ 2: Biến đổi biểu thức 1 + sin 2x – cos 2x – tan 2x thành tích.
Hướng dẫn giải:
1 + sin 2x – cos 2x – tan 2x
= 1 + sin 2x – cos 2x – sin 2x/cos 2x
= [cos 2x (1 + sin 2x) – cos² 2x – sin 2x]/cos 2x
= [sin 2x . (cos 2x – 1) – cos² 2x + cos 2x]/cos 2x
= [sin 2x . (cos 2x – 1) – cos 2x . (cos 2x – 1)]/cos 2x
Ví dụ 3: Biến đổi biểu thức sin x – sin 2x + sin 3x thành tích.
Hướng dẫn giải:
sin x – sin 2x + sin 3x
= sin x – 2 . sin x . cos x + 3 sin x – 4 sin³ x
= – 4 . sin³ x + 4 . sin x – 2 . sin x . cos x
= 2 . sin x . (– 2 sin² x + 2 – cos x)
= 2 . sin x .(– 2 sin² x + 2 sin² x + 2 cos² x – cos x)
= 2 . sin x . (2 cos² x – cos x)
= 2 . sin x . cos x . (2 cos x – 1)
= sin 2x . (2 cos x – 1)
 Ví dụ minh họa biến đổi sin2x thành tích
Ví dụ minh họa biến đổi sin2x thành tích
Alt: Đồ thị hàm số y=sin2x minh họa trực quan sự biến thiên và tính chất của hàm số này, giúp người học dễ dàng hình dung và ghi nhớ.
Ví dụ 4: Chứng minh đẳng thức: sin x . (1 + cos 2x) = sin 2x . cos x
Hướng dẫn giải:
Biến đổi vế trái:
sin x . (1 + cos 2x)
= sin x . 2cos² x (Sử dụng công thức cos 2x = 2cos² x – 1)
= (2 sin x . cos x) . cos x
= sin 2x . cos x (Sử dụng công thức sin 2x = 2 sin x cos x)
Vậy đẳng thức được chứng minh.
B. Hàm Số y = sin 2x
1. Tập Xác Định
Hàm số y = sin 2x có tập xác định là D = R (tất cả các số thực). Điều này có nghĩa là bạn có thể thay bất kỳ giá trị x nào vào hàm số.
2. Tập Giá Trị
Tập giá trị của hàm số y = sin 2x là [-1, 1]. Vì giá trị của sin luôn nằm trong khoảng từ -1 đến 1, nên:
-1 ≤ sin 2x ≤ 1
Giá trị lớn nhất của y = sin 2x là 1.
Giá trị nhỏ nhất của y = sin 2x là -1.
3. Tính Chẵn Lẻ
Để xác định tính chẵn lẻ, ta xét y(-x):
y(-x) = sin(-2x) = -sin(2x) = -y(x)
Vì y(-x) = -y(x), hàm số y = sin 2x là hàm số lẻ.
4. Chu Kỳ Tuần Hoàn
Hàm số y = sin 2x tuần hoàn với chu kỳ T = π. Nói cách khác, đồ thị của hàm số lặp lại sau mỗi khoảng π đơn vị trên trục x.
Công thức mở rộng: Hàm số y = sin (ax + b) tuần hoàn với chu kì T = 2π/|a|.
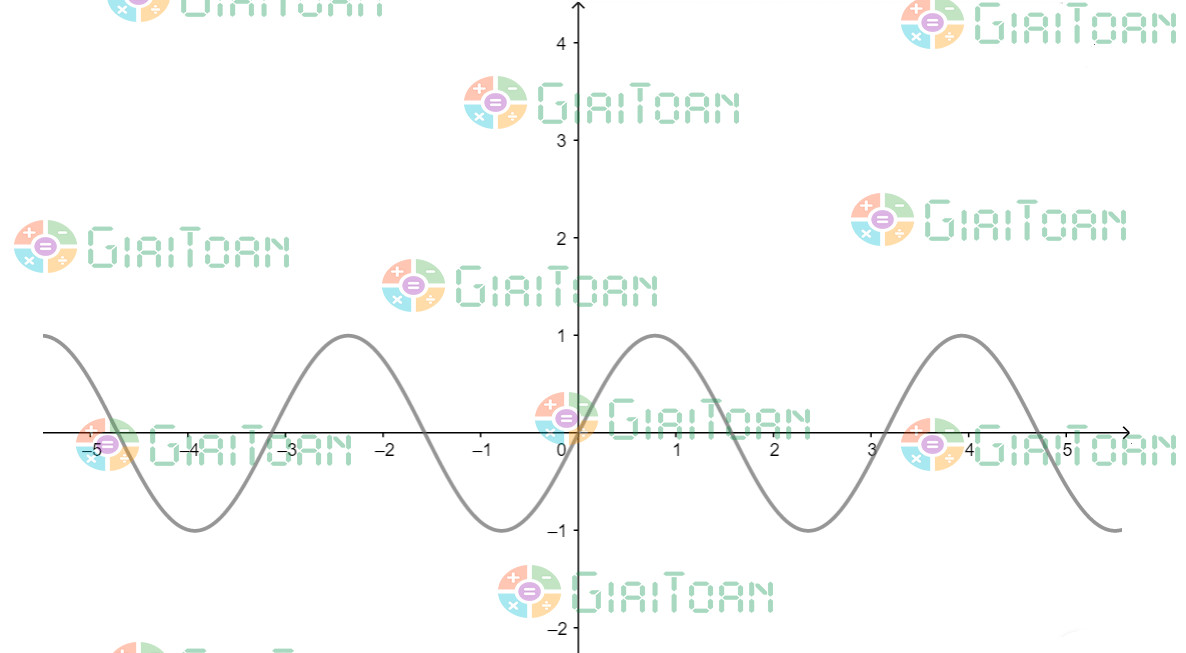
C. Đồ Thị Hàm Số y = sin 2x
Đồ thị của hàm số y = sin 2x có dạng sóng sin, nhưng bị nén lại theo phương ngang so với đồ thị của y = sin x. Chu kỳ của nó là π, ngắn hơn so với chu kỳ 2π của y = sin x.
D. Đạo Hàm của Sin 2x
Để tìm đạo hàm của y = sin 2x, ta sử dụng quy tắc chuỗi:
y = sin 2x
y’ = (sin 2x)’
y’ = (2x)’ . cos 2x
y’ = 2 . cos (2x)
Vậy, đạo hàm của y = sin 2x là y’ = 2 cos (2x).
E. Nguyên Hàm của Sin 2x
Để tìm nguyên hàm của sin 2x, ta thực hiện tích phân:
∫ sin 2x dx = (1/2) ∫ sin 2x d(2x) = – (1/2) cos 2x + C
Vậy họ nguyên hàm của hàm số y = sin 2x là – (1/2) cos 2x + C.
Alt: Công thức tính nguyên hàm của sin2x, một bước quan trọng trong giải tích tích phân, giúp tìm ra họ các hàm số có đạo hàm là sin2x.
F. Ứng Dụng của Sin 2x trong Phương Trình Lượng Giác
Công thức sin 2x được sử dụng rộng rãi trong giải các phương trình lượng giác. Một số dạng phương trình thường gặp:
- sin 2x + cos 2x = 1
- sin 2x + cos 2x = 0
- sin x = cos x
Việc nắm vững công thức sin 2x giúp đơn giản hóa các phương trình và tìm ra nghiệm dễ dàng hơn.
Công thức sin2x là một công cụ mạnh mẽ trong lượng giác và giải tích. Việc hiểu rõ công thức, các tính chất liên quan, và biết cách áp dụng vào các bài toán cụ thể sẽ giúp bạn nâng cao kỹ năng giải toán và ứng dụng vào thực tế.
