Trong chương trình Toán lớp 10, Sin Cos Tan Lớp 10 là nền tảng quan trọng của lượng giác. Việc nắm vững các công thức lượng giác không chỉ giúp bạn giải quyết các bài tập trên lớp mà còn là hành trang cần thiết cho các kỳ thi quan trọng sau này. Bài viết này sẽ tổng hợp đầy đủ các công thức sin cos tan lớp 10 từ cơ bản đến nâng cao, giúp bạn học tập hiệu quả hơn.
Công Thức Lượng Giác Cơ Bản (Sin Cos Tan) Lớp 10
Các công thức lượng giác cơ bản là nền tảng để hiểu sâu hơn về lượng giác. Chúng bao gồm định nghĩa của sin, cos, tan và các hệ thức lượng giác cơ bản khác.
Công Thức Cộng Các Góc Lượng Giác
Công thức cộng giúp tính giá trị lượng giác của tổng hoặc hiệu hai góc. Đây là một công cụ quan trọng để giải quyết các bài toán phức tạp hơn.
Công thức cộng lượng giác có một mẹo nhớ thú vị: “Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ”.
Công Thức Các Cung Liên Kết Đặc Biệt
Các cung liên kết đặc biệt giúp đơn giản hóa việc tính toán bằng cách chuyển đổi giữa các góc có quan hệ đặc biệt với nhau (đối nhau, bù nhau, phụ nhau, hơn kém π/2, hơn kém π).
- Hai góc đối nhau: cos(-x) = cos(x), sin(-x) = -sin(x), tan(-x) = -tan(x)
- Hai góc bù nhau: sin(π – x) = sin(x), cos(π – x) = -cos(x), tan(π – x) = -tan(x)
- Hai góc phụ nhau: sin(π/2 – x) = cos(x), cos(π/2 – x) = sin(x), tan(π/2 – x) = cot(x)
- Hai góc hơn kém π: sin(π + x) = -sin(x), cos(π + x) = -cos(x), tan(π + x) = tan(x)
- Hai góc hơn kém π/2: sin(π/2 + x) = cos(x), cos(π/2 + x) = -sin(x), tan(π/2 + x) = -cot(x)
“Cos đối, sin bù, phụ chéo, tan hơn kém pi” là câu thần chú giúp bạn dễ dàng ghi nhớ các công thức này.
Công Thức Nhân Đôi, Nhân Ba
Công thức nhân đôi và nhân ba cho phép bạn tính giá trị lượng giác của góc gấp đôi hoặc gấp ba một góc đã biết.
Công Thức Hạ Bậc Lượng Giác
Công thức hạ bậc giúp giảm bậc của các hàm lượng giác, thường được sử dụng để đơn giản hóa biểu thức hoặc tính tích phân.
Công Thức Biến Đổi Tổng Thành Tích
Công thức biến đổi tổng thành tích giúp chuyển đổi tổng hoặc hiệu của các hàm lượng giác thành tích, hữu ích trong việc giải phương trình lượng giác.
Mẹo nhớ công thức biến đổi tổng thành tích lượng giác: “cos cộng cos bằng 2 cos cos, cos trừ cos bằng trừ 2 sin sin; sin cộng sin bằng 2 sin cos, sin trừ sin bằng 2 cos sin.”
Nghiệm Của Phương Trình Lượng Giác Cơ Bản
Nắm vững nghiệm của các phương trình lượng giác cơ bản là chìa khóa để giải quyết các bài toán lượng giác phức tạp.
Dấu Của Các Giá Trị Lượng Giác Trong Các Góc Phần Tư
Biết dấu của sin, cos, tan trong các góc phần tư khác nhau giúp xác định giá trị của các hàm lượng giác một cách chính xác.
| Góc phần tư số | I | II | III | IV |
|---|---|---|---|---|
| sin (x) | + | + | – | – |
| cos (x) | + | – | – | + |
| tan (x) | + | – | + | – |
| cot (x) | + | – | + | – |

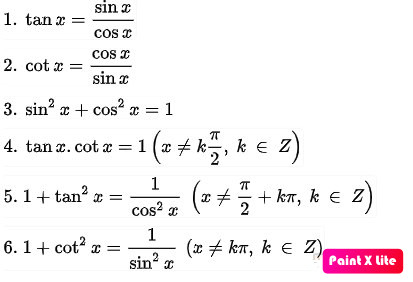


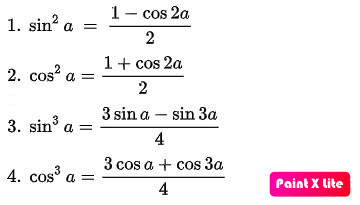

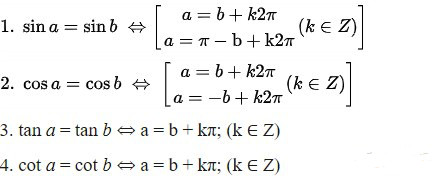
Bảng Giá Trị Lượng Giác Của Một Số Góc Đặc Biệt
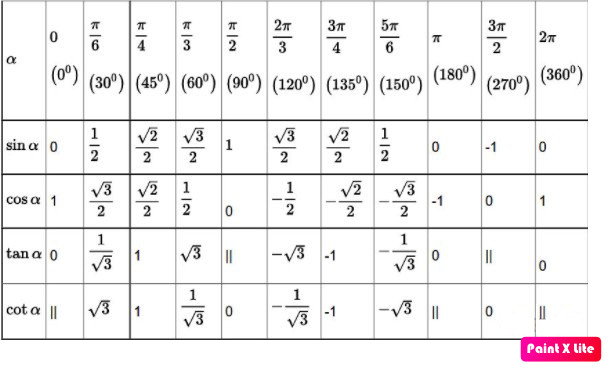
Bảng giá trị lượng giác của các góc đặc biệt (0°, 30°, 45°, 60°, 90°) là kiến thức cơ bản cần phải ghi nhớ.
Bài Thơ Ghi Nhớ Công Thức Lượng Giác Lớp 10
Học thuộc các bài thơ vần điệu giúp việc ghi nhớ công thức lượng giác trở nên dễ dàng và thú vị hơn rất nhiều.
Công thức cộng:
- Cos cộng cos bằng 2 cos cos
- cos trừ cos bằng trừ 2 sin sin
- Sin cộng sin bằng 2 sin cos
- sin trừ sin bằng 2 cos sin.
Các cung liên quan đặc biệt:
- Cos đối, sin bù, phụ chéo, tan hơn kém pi
Biến đổi tích thành tổng:
- Cos cos nửa cos-+, + cos-trừ
- Sin sin nửa cos-trừ trừ cos-+
- Sin cos nửa sin-+ + sin-trừ
Hy vọng với tổng hợp chi tiết các công thức sin cos tan lớp 10 này, các bạn học sinh sẽ nắm vững kiến thức và tự tin chinh phục các bài toán lượng giác. Chúc các bạn học tốt!

