Khám phá sâu về hình chóp tứ giác đều, từ định nghĩa cơ bản đến các công thức tính toán diện tích, thể tích và bài tập vận dụng.
1. Định Nghĩa Hình Chóp Tứ Giác Đều
Hình chóp tứ giác đều là hình chóp có đáy là hình vuông và đường cao của hình chóp đi qua tâm của đáy (giao điểm của hai đường chéo hình vuông).
Ảnh minh họa khối chóp tứ giác đều, với đáy hình vuông và đường cao đi qua tâm đáy, giúp người đọc dễ hình dung về khái niệm này.
2. Các Tính Chất Quan Trọng của Hình Chóp Tứ Giác Đều
Hình chóp tứ giác đều sở hữu những tính chất đặc trưng sau:
- Các cạnh bên bằng nhau.
- Mặt đáy là hình vuông.
- Chân đường cao trùng với tâm của mặt đáy.
- Các mặt bên là các tam giác cân bằng nhau.
- Các góc tạo bởi cạnh bên và mặt đáy bằng nhau.
- Các góc tạo bởi các mặt bên và mặt đáy bằng nhau.
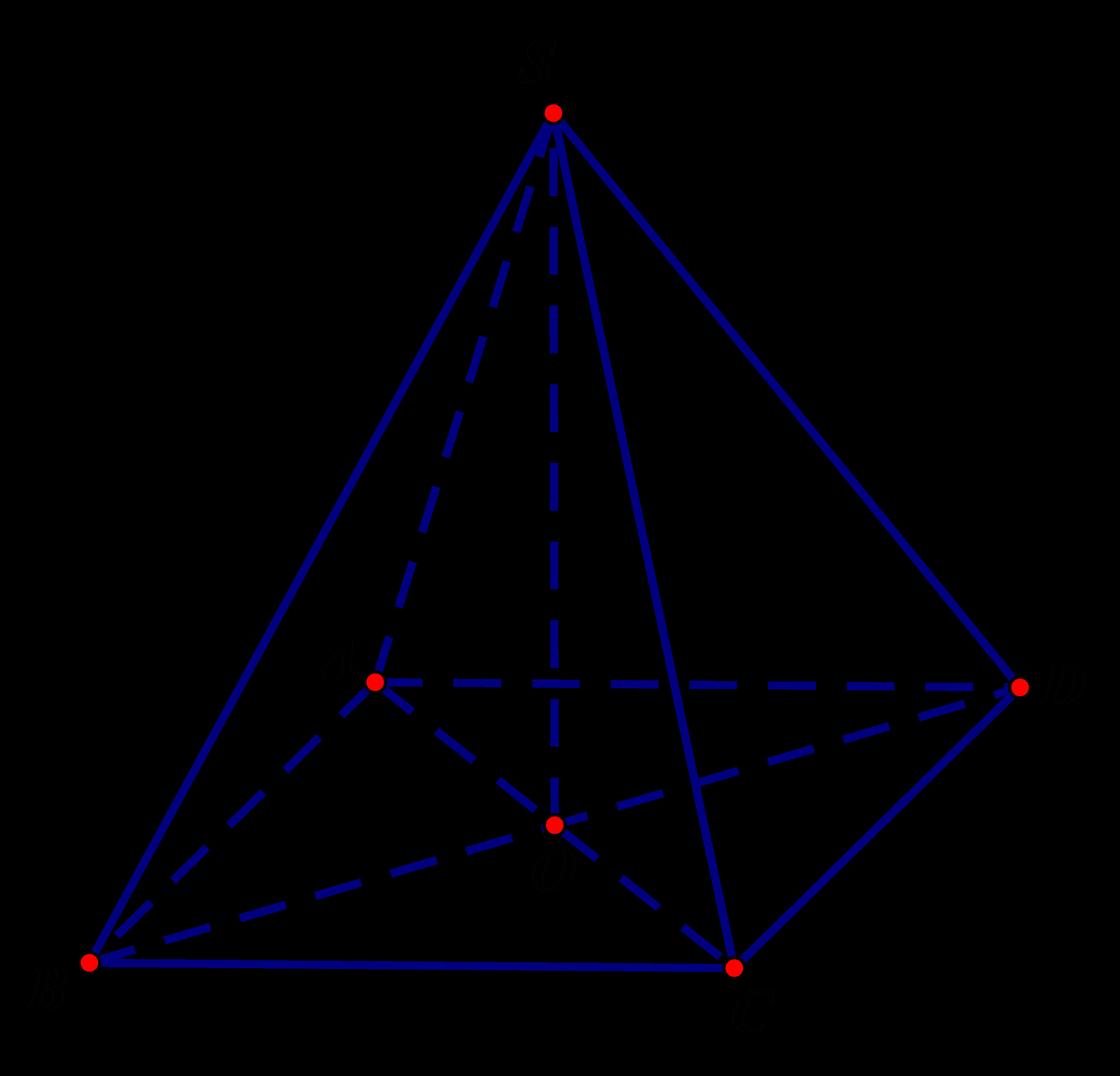
Ví dụ, xét hình chóp tứ giác đều SABCD, ta có:
- Tứ giác ABCD là hình vuông với tâm O.
- SO vuông góc với mặt phẳng (ABCD).
- SA = SB = SC = SD.
- Góc giữa (SA; (ABCD)) = (SD;(ABCD))= (SB;(ABCD))=(SC;(ABCD)).
Hình ảnh minh họa hình chóp tứ giác đều SABCD, thể hiện rõ các đỉnh, cạnh đáy và cạnh bên, giúp người đọc hiểu rõ hơn về cấu trúc hình học.
3. Công Thức Tính Thể Tích Hình Chóp Tứ Giác Đều
Thể tích (V) của hình chóp tứ giác đều được tính theo công thức:
V = (1/3) Sđáy h
Trong đó:
- V: Thể tích của hình chóp tứ giác đều.
- h: Chiều cao của hình chóp tứ giác đều.
- Sđáy: Diện tích của đáy hình chóp tứ giác đều.
4. Công Thức Tính Diện Tích Hình Chóp Tứ Giác Đều
4.1. Diện Tích Xung Quanh
Diện tích xung quanh (Sxq) của hình chóp tứ giác đều được tính như sau:
Sxq = 4 * S
Trong đó:
- Sxq: Diện tích xung quanh của hình chóp tứ giác đều.
- S: Diện tích một mặt bên của hình chóp tứ giác đều.
Ảnh minh họa cách tính diện tích xung quanh của hình chóp tứ giác đều, bằng tổng diện tích của bốn mặt bên hình tam giác cân.
4.2. Diện Tích Toàn Phần
Diện tích toàn phần (Stp) của hình chóp tứ giác đều được tính bằng công thức:
Stp = Sxq + Sđáy
Trong đó:
- Stp: Diện tích toàn phần của hình chóp tứ giác đều.
- Sxq: Diện tích xung quanh của hình chóp tứ giác đều.
- Sđáy: Diện tích đáy của hình chóp tứ giác đều.
5. Bài Tập Vận Dụng Tính Thể Tích Hình Chóp Tứ Giác Đều (Có Lời Giải)
Câu 1: Cho hình chóp đều S.ABCD có AB = a, SA = a. Tính thể tích khối chóp S.ABCD.
Giải:
- Đáy ABCD là hình vuông cạnh a, nên S(ABCD) = a².
- Gọi H là tâm của hình vuông ABCD. Tam giác SHA vuông tại H, ta có:
SH = √(SA² – AH²) = a√2 / 2 - Vậy thể tích khối chóp S.ABCD là:
V(S.ABCD) = (1/3) S(ABCD) SH = a³√2 / 6
Câu 2: Tính thể tích khối chóp tứ giác đều có tất cả các cạnh bằng a.
Giải:
- Diện tích đáy ABCD là a².
- Gọi O là tâm đáy. SO² = SB² – OB² = a² – (a√2 / 2)² = a² / 2
- Suy ra: SO = a√2 / 2
- Thể tích khối chóp là: V(S.ABCD) = (1/3) (a√2 / 2) a² = a³√2 / 6
Câu 3: Cho hình chóp tứ giác đều có cạnh đáy bằng x. Diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích khối chóp.
Giải:
- Thể tích khối chóp: V = (1/3) B h, với B = x²
- Gọi O là tâm hình vuông, I là trung điểm CD => SI vuông góc CD.
- Gọi SO = h => SI = √(SO² + OI²) = √(h² + x²/4)
- Sxq = 2 SI CD; Sxq = 2B => 2x√(h² + x²/4) = 2x² => √(h² + x²/4) = x
- Suy ra: h² + x²/4 = x² => h² = 3x²/4 => h = x√3 / 2
- Vậy V = (1/3) x² (x√3 / 2) = x³√3 / 6
Câu 4: Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với đáy góc 60 độ. Tính thể tích hình chóp đều S.ABCD.
Giải:
- Gọi O là giao điểm của AC và BD => SO ⊥ (ABCD)
- => widehat{SCO} = 60^{0} => tan60^{0} = frac{SO}{OC} => SO = OCsqrt{3} = frac{a}{sqrt{2}}.sqrt{3}
- => V = frac{1}{3}asqrt{tfrac{3}{2}}.a^{2} = frac{a^{3}sqrt{6}}{6}
Câu 5: Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp 2 lần cạnh đáy. Tính thể tích khối chóp tứ giác đã cho.
Giải:
- Ta có AC = asqrt{2} => AO = frac{asqrt{2}}{2} => SO = sqrt{SA^{2} – OA^{2}} = frac{asqrt{14}}{2}
- Vậy V{S.ABCD} = frac{1}{3}SO.S{ABCD} = frac{1}{3}.frac{sqrt{14}}{2}.a^{3} = frac{sqrt{14}}{6}a^{3}
Câu 6: Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng asqrt{3}. Tính thể tích của hình chóp đó theo a.
Giải:
- Gọi h là chiều cao của hình chóp đã cho, ta có:
- h = sqrt{3a^{2} – frac{a^{2}}{2}} = frac{asqrt{10}}{2}
- V = frac{1}{3}S_{ABCD}.h = frac{1}{3}a^{2}.frac{asqrt{10}}{2} = frac{a^{3}sqrt{10}}{6}
Câu 7: Chó hình chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng a. Tính thể tích khối chóp đó.
Giải:
- Xét hình chóp tứ giác đều S.ABCD
- Ta có: OD = frac{asqrt{2}}{2}, SO = sqrt{SD^{2} – OD^{2}} = sqrt{2a^{2} – frac{a^{2}}{2}} = frac{asqrt{6}}{2}
- V{S.ABCD} = frac{1}{3}.SO.S{ABCD} = frac{1}{3}.frac{asqrt{6}}{2}.a^{2} = frac{a^{3}sqrt{6}}{6}
Hy vọng với những kiến thức và bài tập trên, bạn sẽ nắm vững về hình chóp tứ giác đều và các ứng dụng của nó.