Trong hình học, tam giác vuông là một hình cơ bản nhưng lại vô cùng quan trọng, xuất hiện rất nhiều trong các bài toán và ứng dụng thực tế. Để giải quyết các bài toán liên quan đến tam giác vuông, việc nắm vững công thức tính diện tích tam giác vuông là vô cùng cần thiết. Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ và chi tiết nhất về chủ đề này, giúp bạn tự tin chinh phục mọi bài toán về diện tích tam giác vuông.
Công Thức Tính Diện Tích Tam Giác Vuông Cơ Bản
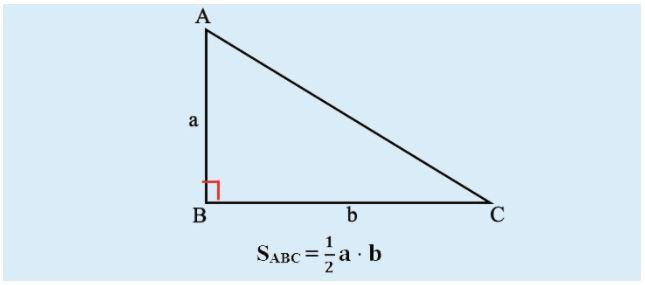
Tam giác vuông là tam giác có một góc vuông (90 độ). Hai cạnh tạo thành góc vuông được gọi là cạnh góc vuông, cạnh còn lại (đối diện góc vuông) là cạnh huyền. Công thức tính diện tích tam giác vuông đơn giản nhất là:
S = (1/2) a b
Trong đó:
- S là diện tích tam giác vuông
- a và b là độ dài hai cạnh góc vuông
Ngoài ra, bạn có thể áp dụng công thức diện tích tam giác tổng quát nếu biết một cạnh và chiều cao tương ứng:
S = (1/2) h c
Trong đó:
- h là chiều cao của tam giác (đường vuông góc hạ từ đỉnh đến cạnh đáy)
- c là độ dài cạnh đáy
Công Thức Tính Diện Tích Tam Giác Vuông Cân
Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau. Diện tích tam giác vuông cân có thể được tính nhanh chóng bằng công thức:
*S = (1/2) a²**
Trong đó:
- S là diện tích tam giác vuông cân
- a là độ dài cạnh góc vuông
Các Trường Hợp Đặc Biệt và Mở Rộng
Ngoài công thức cơ bản, đôi khi bạn sẽ cần áp dụng các kiến thức khác để tính diện tích tam giác vuông trong những trường hợp phức tạp hơn:
- Sử dụng định lý Pythagoras: Nếu chỉ biết độ dài một cạnh góc vuông và cạnh huyền, bạn có thể sử dụng định lý Pythagoras (a² + b² = c²) để tìm độ dài cạnh góc vuông còn lại, sau đó áp dụng công thức tính diện tích tam giác vuông.
- Sử dụng các tỉ số lượng giác: Nếu biết một cạnh và một góc nhọn, bạn có thể sử dụng các tỉ số lượng giác (sin, cos, tan) để tìm độ dài cạnh còn lại, sau đó áp dụng công thức tính diện tích tam giác vuông.
- Tam giác vuông trong hệ tọa độ Oxyz: Nếu tam giác vuông được cho trong không gian Oxyz, bạn cần tìm tọa độ các đỉnh của tam giác, sau đó sử dụng tích có hướng của hai vectơ cạnh góc vuông để tính diện tích.
Bài Tập Vận Dụng và Ví Dụ Minh Họa
Để hiểu rõ hơn về cách tính diện tích tam giác vuông, hãy cùng xem xét một số ví dụ sau:
Ví dụ 1: Cho tam giác ABC vuông tại A, có AB = 6cm và AC = 8cm. Tính diện tích tam giác ABC.
Giải:
Áp dụng công thức S = (1/2) a b, ta có:
S = (1/2) 6 8 = 24 cm²
Ví dụ 2: Cho tam giác vuông cân có cạnh góc vuông bằng 5cm. Tính diện tích tam giác.
Giải:
Áp dụng công thức S = (1/2) a², ta có:
S = (1/2) 5² = 12.5 cm²
Ví dụ 3: Cho tam giác ABC vuông tại A, cạnh huyền BC = 10cm và cạnh AB = 6cm. Tính diện tích tam giác ABC.
Giải:
Áp dụng định lý Pythagoras: AC² = BC² – AB² = 10² – 6² = 64 => AC = 8cm
Áp dụng công thức S = (1/2) a b, ta có:
S = (1/2) 6 8 = 24 cm²
Ứng Dụng Thực Tế của Diện Tích Tam Giác Vuông
Kiến thức về diện tích tam giác vuông không chỉ hữu ích trong các bài toán hình học mà còn có nhiều ứng dụng thực tế trong cuộc sống, ví dụ như:
- Xây dựng và kiến trúc: Tính toán diện tích mái nhà, tường nhà, các chi tiết trang trí có hình tam giác.
- Thiết kế: Thiết kế các vật dụng, đồ nội thất có hình tam giác.
- Địa lý: Tính toán diện tích các khu vực có hình dạng gần đúng với tam giác.
- Toán học và khoa học: Sử dụng trong các bài toán liên quan đến vector, tích phân, vật lý.
Lưu Ý Quan Trọng Khi Tính Diện Tích Tam Giác Vuông
- Luôn đảm bảo các đơn vị đo độ dài là nhất quán trước khi thực hiện phép tính.
- Kiểm tra kỹ đề bài để xác định thông tin đã cho và lựa chọn công thức phù hợp.
- Trong các bài toán phức tạp, nên vẽ hình để dễ dàng hình dung và áp dụng các định lý, công thức.
Kết Luận
Nắm vững công thức tính diện tích tam giác vuông là một kỹ năng quan trọng trong học tập và ứng dụng thực tế. Hy vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức cần thiết để tự tin giải quyết mọi bài toán liên quan đến diện tích tam giác vuông. Hãy luyện tập thường xuyên để thành thạo các công thức và ứng dụng chúng một cách linh hoạt!