Elip là một trong những đường conic quan trọng trong hình học giải tích. Bài viết này sẽ cung cấp một cái nhìn toàn diện về “Pt Elip”, từ định nghĩa cơ bản đến các dạng bài tập thường gặp và cách giải quyết chúng.
1. Định Nghĩa và Các Yếu Tố Cơ Bản của Elip
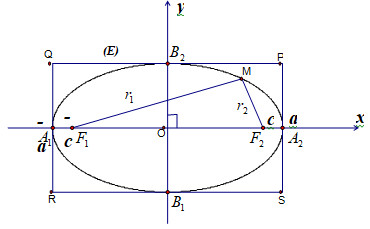
Trong mặt phẳng, cho hai điểm cố định $F_1$ và $F_2$ gọi là tiêu điểm. Elip là tập hợp các điểm M sao cho tổng khoảng cách từ M đến hai tiêu điểm là một hằng số: $MF_1 + MF_2 = 2a$, với a là một số dương cho trước. Khoảng cách giữa hai tiêu điểm, $F_1F_2 = 2c$, được gọi là tiêu cự của elip.
2. Phương Trình Chính Tắc của Elip
Để đơn giản hóa việc nghiên cứu, ta chọn hệ trục tọa độ Oxy sao cho hai tiêu điểm nằm trên trục hoành và đối xứng qua gốc tọa độ, tức là $F_1(-c; 0)$ và $F_2(c; 0)$. Khi đó, phương trình của elip có dạng:
$frac{x^2}{a^2} + frac{y^2}{b^2} = 1$
Trong đó:
- a là độ dài bán trục lớn
- b là độ dài bán trục bé
- $c^2 = a^2 – b^2$
Phương trình này được gọi là phương trình chính tắc của elip.
Hình ảnh minh họa phương trình chính tắc của elip, thể hiện rõ các yếu tố a, b, x, y.
Ví dụ: Viết phương trình chính tắc của elip (E) biết độ dài trục lớn bằng 8 và độ dài trục bé bằng 6.
Giải:
Ta có: $2a = 8 Rightarrow a = 4$ và $2b = 6 Rightarrow b = 3$.
Vậy phương trình chính tắc của elip (E) là: $frac{x^2}{16} + frac{y^2}{9} = 1$
3. Hình Dạng và Các Thành Phần Của Elip
Từ phương trình chính tắc, ta có thể suy ra hình dạng và các thành phần quan trọng của elip:
- Tính đối xứng: Elip đối xứng qua trục Ox, trục Oy và gốc tọa độ O.
- Các đỉnh: Elip cắt trục Ox tại $A_1(-a; 0)$ và $A_2(a; 0)$, cắt trục Oy tại $B_1(0; -b)$ và $B_2(0; b)$. $A_1, A_2, B_1, B_2$ được gọi là các đỉnh của elip.
- Trục lớn: Đoạn thẳng $A_1A_2$ có độ dài 2a.
- Trục bé: Đoạn thẳng $B_1B_2$ có độ dài 2b.
Hình ảnh minh họa các thành phần của elip như trục lớn, trục bé, tâm sai và các đỉnh, giúp người đọc hình dung rõ hơn về cấu trúc của elip.
Ví dụ: Cho elip (E) có phương trình: $frac{x^2}{25} + frac{y^2}{9} = 1$. Xác định độ dài các trục, tọa độ các tiêu điểm và các đỉnh của elip.
Giải:
Từ phương trình, ta có $a^2 = 25 Rightarrow a = 5$ và $b^2 = 9 Rightarrow b = 3$.
Suy ra $c = sqrt{a^2 – b^2} = sqrt{25 – 9} = 4$.
Vậy:
- Độ dài trục lớn: $2a = 10$
- Độ dài trục bé: $2b = 6$
- Tiêu điểm: $F_1(-4; 0)$ và $F_2(4; 0)$
- Các đỉnh: $A_1(-5; 0)$, $A_2(5; 0)$, $B_1(0; -3)$, $B_2(0; 3)$
Hình ảnh minh họa đồ thị elip trên hệ trục tọa độ, thể hiện rõ cách xác định các yếu tố quan trọng như bán trục lớn, bán trục bé và vị trí của các tiêu điểm.
4. Các Dạng Bài Tập Thường Gặp Về Phương Trình Elip và Cách Giải
Dạng 1: Viết phương trình chính tắc của elip khi biết các yếu tố liên quan.
- Ví dụ: Elip (E) có một tiêu điểm $F_1(-sqrt{5}; 0)$ và đi qua điểm $M(2; frac{3}{5}sqrt{5})$. Viết phương trình chính tắc của (E).
Cách giải:
- Từ tiêu điểm, ta có $c = sqrt{5}$.
- Gọi phương trình elip là $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$.
- Vì M thuộc elip nên $frac{4}{a^2} + frac{9}{5b^2} = 1$.
- Kết hợp với $a^2 – b^2 = c^2 = 5$, ta giải hệ phương trình để tìm a và b.
Dạng 2: Tìm tọa độ điểm trên elip thỏa mãn điều kiện cho trước.
- Ví dụ: Cho elip (E): $frac{x^2}{16} + frac{y^2}{9} = 1$. Tìm điểm M trên (E) sao cho M nhìn hai tiêu điểm dưới một góc vuông.
Cách giải:
- Gọi $M(x_0; y_0)$. Viết phương trình các vectơ $overrightarrow{MF_1}$ và $overrightarrow{MF_2}$.
- Sử dụng điều kiện góc vuông: $overrightarrow{MF_1} cdot overrightarrow{MF_2} = 0$.
- Kết hợp với phương trình elip $frac{x_0^2}{16} + frac{y_0^2}{9} = 1$, ta giải hệ phương trình để tìm $x_0$ và $y_0$.
Dạng 3: Bài toán liên quan đến tiếp tuyến của elip.
- Ví dụ: Cho elip (E): $frac{x^2}{4} + y^2 = 1$. Viết phương trình tiếp tuyến của (E) tại điểm $A(1; frac{sqrt{3}}{2})$.
Cách giải:
- Phương trình tiếp tuyến tại điểm $A(x_0; y_0)$ trên elip là: $frac{x_0x}{a^2} + frac{y_0y}{b^2} = 1$.
- Thay tọa độ điểm A và các giá trị a, b vào phương trình trên.
Dạng 4: Ứng dụng phương trình elip để giải các bài toán hình học phẳng.
Hình ảnh minh họa bài toán liên quan đến elip và đường tròn, thể hiện sự tương quan giữa hai hình và cách giải quyết bài toán bằng phương pháp hình học giải tích.
- Ví dụ: Cho đường tròn (C): $x^2 + y^2 = 4$ và elip (E): $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$. Tìm a và b để (E) tiếp xúc với (C) tại 4 điểm tạo thành hình vuông.
Cách giải:
- Sử dụng điều kiện tiếp xúc giữa elip và đường tròn.
- Sử dụng tính chất hình vuông để thiết lập các phương trình liên quan đến a và b.
- Giải hệ phương trình để tìm a và b.
5. Kết Luận
Hiểu rõ “pt elip” không chỉ giúp giải quyết các bài toán hình học giải tích mà còn là nền tảng quan trọng để tiếp cận các khái niệm toán học cao cấp hơn. Việc luyện tập thường xuyên với nhiều dạng bài tập khác nhau sẽ giúp bạn nắm vững kiến thức và ứng dụng một cách linh hoạt.