Phương Trình Oxy, hay còn gọi là mặt phẳng tọa độ Oxy, là một khái niệm cơ bản trong hình học giải tích, đặc biệt quan trọng trong chương trình Toán học phổ thông và cao cấp. Bài viết này sẽ cung cấp một cái nhìn tổng quan về phương trình Oxy, bao gồm định nghĩa, cách xác định phương trình, các dạng bài tập thường gặp và ứng dụng thực tế.
1. Định Nghĩa và Ý Nghĩa của Phương Trình Oxy
Trong không gian Oxyz, mặt phẳng Oxy là mặt phẳng chứa hai trục tọa độ Ox và Oy. Mặt phẳng này vuông góc với trục Oz tại gốc tọa độ O. Mọi điểm nằm trên mặt phẳng Oxy đều có tọa độ z bằng 0.
Phương trình tổng quát của mặt phẳng Oxy:
z = 0
Phương trình này thể hiện rằng, bất kỳ điểm nào thuộc mặt phẳng Oxy đều có cao độ (tọa độ z) bằng 0. Đây là một trong những phương trình mặt phẳng cơ bản nhất trong không gian ba chiều.
2. Cách Xác Định Phương Trình Mặt Phẳng Oxy
Để xác định phương trình mặt phẳng Oxy, ta dựa vào tính chất các điểm nằm trên mặt phẳng này có tọa độ z bằng 0. Do đó, phương trình của mặt phẳng Oxy là z = 0.
Ví dụ:
Cho điểm A(1; 2; 0), điểm này thuộc mặt phẳng Oxy vì có tọa độ z = 0.
Điểm B(3; -1; 5) không thuộc mặt phẳng Oxy vì tọa độ z ≠ 0.
3. Các Dạng Bài Tập Thường Gặp Liên Quan Đến Phương Trình Oxy
Các bài tập liên quan đến phương trình Oxy thường xuất hiện dưới nhiều dạng khác nhau, đòi hỏi học sinh nắm vững kiến thức cơ bản và khả năng vận dụng linh hoạt. Dưới đây là một số dạng bài tập thường gặp:
- Xác định điểm thuộc/không thuộc mặt phẳng Oxy: Cho một điểm và yêu cầu xác định xem điểm đó có thuộc mặt phẳng Oxy hay không.
- Tìm giao tuyến của mặt phẳng với mặt phẳng Oxy: Cho một mặt phẳng và yêu cầu tìm giao tuyến của nó với mặt phẳng Oxy.
- Viết phương trình mặt phẳng song song hoặc vuông góc với mặt phẳng Oxy: Cho một điểm và yêu cầu viết phương trình mặt phẳng đi qua điểm đó và song song hoặc vuông góc với mặt phẳng Oxy.
- Tính khoảng cách từ một điểm đến mặt phẳng Oxy: Cho một điểm và yêu cầu tính khoảng cách từ điểm đó đến mặt phẳng Oxy.
Ví dụ 1:
Cho điểm M(2; -3; 0). Hỏi điểm M có thuộc mặt phẳng Oxy không? Vì sao?
Giải:
Điểm M thuộc mặt phẳng Oxy vì tọa độ z của M bằng 0.
Ví dụ 2:
Viết phương trình mặt phẳng đi qua điểm A(1; 2; 3) và song song với mặt phẳng Oxy.
Giải:
Mặt phẳng song song với mặt phẳng Oxy có dạng z = c, với c là hằng số. Vì mặt phẳng này đi qua điểm A(1; 2; 3), nên ta có c = 3. Vậy phương trình mặt phẳng cần tìm là z = 3.
4. Ứng Dụng của Phương Trình Oxy
Phương trình Oxy không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:
- Trong hình học: Mặt phẳng Oxy là hệ quy chiếu cơ bản để xác định vị trí và tính toán các đặc tính của các hình hình học trong không gian.
- Trong đồ họa máy tính: Mặt phẳng Oxy được sử dụng để biểu diễn các đối tượng 2D và là cơ sở để xây dựng các mô hình 3D.
- Trong kỹ thuật và xây dựng: Phương trình Oxy giúp kỹ sư và kiến trúc sư xác định và tính toán các yếu tố liên quan đến mặt phẳng ngang trong thiết kế và xây dựng công trình.
- Trong địa lý và bản đồ: Mặt phẳng Oxy được sử dụng để biểu diễn các khu vực địa lý trên bản đồ và giúp xác định vị trí các đối tượng trên bề mặt Trái Đất.
5. Mở Rộng Kiến Thức: Các Mặt Phẳng Tọa Độ Khác
Tương tự như mặt phẳng Oxy, ta có các mặt phẳng tọa độ khác trong không gian Oxyz:
- Mặt phẳng Oyz: Là mặt phẳng chứa hai trục Oy và Oz. Phương trình của mặt phẳng Oyz là x = 0.
- Mặt phẳng Ozx: Là mặt phẳng chứa hai trục Oz và Ox. Phương trình của mặt phẳng Ozx là y = 0.
Hiểu rõ về các mặt phẳng tọa độ giúp chúng ta dễ dàng hình dung và giải quyết các bài toán liên quan đến hình học không gian.
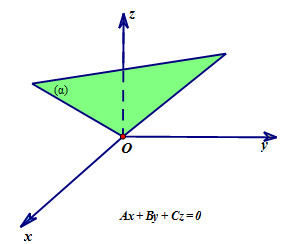Mô tả hệ trục tọa độ Oxyz và các mặt phẳng tọa độ Oxy, Oyz, Ozx
Hệ trục tọa độ Oxyz với các mặt phẳng Oxy (z=0), Oyz (x=0) và Ozx (y=0) được biểu diễn trực quan.
6. Bài Tập Vận Dụng Nâng Cao
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo các bài tập vận dụng sau:
- Cho điểm A(3; -2; 1). Tìm hình chiếu vuông góc của A lên mặt phẳng Oxy.
- Viết phương trình mặt phẳng đi qua ba điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 0). Xác định giao tuyến của mặt phẳng này với mặt phẳng Oxy.
- Tính thể tích khối chóp có đáy là hình vuông nằm trên mặt phẳng Oxy và đỉnh nằm trên trục Oz.
Kết Luận
Phương trình Oxy là một công cụ quan trọng trong hình học giải tích và có nhiều ứng dụng trong thực tế. Việc nắm vững kiến thức cơ bản và rèn luyện kỹ năng giải bài tập sẽ giúp bạn tự tin hơn trong học tập và ứng dụng toán học vào các lĩnh vực khác nhau. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và hữu ích về phương trình Oxy.
