Trong hình học không gian, Phương Trình Mặt Phẳng Trung Trực Của đoạn Thẳng Ab là một khái niệm quan trọng, thường xuyên xuất hiện trong các bài toán liên quan đến tọa độ và khoảng cách. Bài viết này sẽ cung cấp cho bạn một cái nhìn toàn diện về phương trình mặt phẳng trung trực, từ định nghĩa, tính chất đến phương pháp thiết lập và các bài tập ứng dụng.
1. Định Nghĩa và Tính Chất Của Mặt Phẳng Trung Trực
1.1. Định Nghĩa Mặt Phẳng Trung Trực
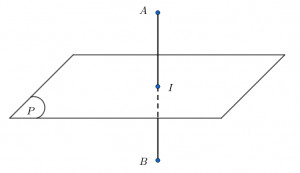
Cho đoạn thẳng AB và điểm I là trung điểm của AB. Mặt phẳng (P) được gọi là mặt phẳng trung trực của đoạn thẳng AB nếu nó đi qua điểm I và vuông góc với đường thẳng AB.
Alt: Mặt phẳng trung trực vuông góc với đoạn thẳng AB tại trung điểm I
1.2. Tính Chất Quan Trọng Của Mặt Phẳng Trung Trực
Mọi điểm nằm trên mặt phẳng trung trực của đoạn thẳng AB đều cách đều hai điểm A và B. Tính chất này là cơ sở để giải nhiều bài toán liên quan đến khoảng cách và quỹ tích điểm.
Alt: Điểm M nằm trên mặt phẳng trung trực nên MA = MB
2. Phương Pháp Viết Phương Trình Mặt Phẳng Trung Trực
Để viết phương trình mặt phẳng trung trực của đoạn thẳng AB, ta thực hiện theo các bước sau:
Bước 1: Xác định tọa độ trung điểm I của đoạn thẳng AB. Tọa độ điểm I được tính bằng công thức:
- $x_I = frac{x_A + x_B}{2}$
- $y_I = frac{y_A + y_B}{2}$
- $z_I = frac{z_A + z_B}{2}$
Bước 2: Tìm vectơ pháp tuyến của mặt phẳng trung trực. Vectơ $overrightarrow{AB}$ chính là vectơ pháp tuyến của mặt phẳng trung trực (P). Tính tọa độ vectơ $overrightarrow{AB}$ bằng công thức:
- $overrightarrow{AB} = (x_B – x_A; y_B – y_A; z_B – z_A)$
Bước 3: Viết phương trình mặt phẳng (P) đi qua điểm I và có vectơ pháp tuyến là $overrightarrow{AB}$. Phương trình tổng quát của mặt phẳng (P) có dạng:
- $A(x – x_I) + B(y – y_I) + C(z – z_I) = 0$,
trong đó (A; B; C) là tọa độ của vectơ $overrightarrow{AB}$.
Ví dụ: Cho điểm A(1; 2; 3) và điểm B(3; 6; 1). Viết phương trình mặt phẳng trung trực (P) của đoạn thẳng AB.
Giải:
- Tìm trung điểm I của AB:
- $x_I = (1 + 3) / 2 = 2$
- $y_I = (2 + 6) / 2 = 4$
- $z_I = (3 + 1) / 2 = 2$
=> I(2; 4; 2)
- Tìm vectơ AB:
- $overrightarrow{AB} = (3 – 1; 6 – 2; 1 – 3) = (2; 4; -2)$
- Viết phương trình mặt phẳng (P):
- $2(x – 2) + 4(y – 4) – 2(z – 2) = 0$
- <=> $2x + 4y – 2z – 16 = 0$
- <=> $x + 2y – z – 8 = 0$
Vậy phương trình mặt phẳng trung trực của đoạn thẳng AB là: $x + 2y – z – 8 = 0$.
3. Bài Tập Vận Dụng
Bài 1: Trong không gian Oxyz, cho hai điểm A(2; 3; 7) và B(4; 1; 3). Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.
Alt: Công thức và cách tính tọa độ trung điểm M và vectơ AB
Giải:
Gọi M là trung điểm của đoạn thẳng AB. Ta có:
- $x_M = (2 + 4) / 2 = 3$
- $y_M = (3 + 1) / 2 = 2$
- $z_M = (7 + 3) / 2 = 5$
=> M(3; 2; 5)
Vectơ $overrightarrow{AB} = (4 – 2; 1 – 3; 3 – 7) = (2; -2; -4)$
Vậy phương trình mặt phẳng trung trực (P) của đoạn thẳng AB là:
Alt: Thiết lập phương trình mặt phẳng trung trực đi qua M và vuông góc với AB
$2(x – 3) – 2(y – 2) – 4(z – 5) = 0$
<=> $2x – 2y – 4z + 18 = 0$
<=> $x – y – 2z + 9 = 0$
Bài 2: Cho M(1; 1; 1), N(4; 3; 2), P(5; 2; 1). Viết phương trình tổng quát của mặt phẳng (MNP).
Alt: Tính tích có hướng của hai vectơ MN và MP để tìm vectơ pháp tuyến
Giải:
Ta có: $overrightarrow{MN} = (3; 2; 1)$ và $overrightarrow{MP} = (4; 1; 0)$.
Vectơ pháp tuyến của mặt phẳng (MNP) là: $overrightarrow{n} = [overrightarrow{MN}, overrightarrow{MP}] = (-1; 4; -5)$
Phương trình mặt phẳng (MNP) là:
$-1(x – 1) + 4(y – 1) – 5(z – 1) = 0$
<=> $-x + 4y – 5z + 2 = 0$
<=> $x – 4y + 5z – 2 = 0$
4. Mẹo Nhỏ Khi Giải Bài Tập Trắc Nghiệm
Khi giải bài tập trắc nghiệm, bạn có thể áp dụng phương pháp loại trừ bằng cách kiểm tra xem các điểm A, B có cách đều các điểm trên mặt phẳng trung trực không. Hoặc, bạn có thể thay tọa độ trung điểm I vào các phương trình đáp án để kiểm tra.
Nắm vững kiến thức về phương trình mặt phẳng trung trực của đoạn thẳng AB sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán hình học không gian trong chương trình học và kỳ thi quan trọng. Chúc bạn học tốt!