Mặt phẳng Oyz là một trong ba mặt phẳng tọa độ cơ bản trong hệ tọa độ Oxyz, đóng vai trò quan trọng trong hình học giải tích không gian. Bài viết này sẽ trình bày chi tiết về Phương Trình Mặt Phẳng Oyz, các dạng bài tập liên quan và ứng dụng của nó.
1. Phương trình mặt phẳng Oyz là gì?
Trong hệ tọa độ Oxyz, mặt phẳng Oyz là mặt phẳng chứa trục Oy và trục Oz. Đặc điểm nổi bật của mặt phẳng này là mọi điểm nằm trên mặt phẳng Oyz đều có hoành độ (giá trị x) bằng 0. Do đó, phương trình mặt phẳng Oyz có dạng đơn giản như sau:
x = 0
Đây là phương trình chính tắc của mặt phẳng Oyz. Mọi điểm có tọa độ (0; y; z) đều thuộc mặt phẳng này, với y và z là các số thực bất kỳ.
2. Véctơ pháp tuyến của mặt phẳng Oyz
Một vectơ pháp tuyến của mặt phẳng Oyz là vectơ vuông góc với mặt phẳng đó. Vì mặt phẳng Oyz có phương trình x = 0, vectơ pháp tuyến của nó có thể được chọn là vectơ đơn vị theo trục Ox, tức là:
n = (1; 0; 0)
Bất kỳ vectơ nào cùng phương với vectơ n cũng là một vectơ pháp tuyến của mặt phẳng Oyz.
3. Các dạng bài tập thường gặp liên quan đến phương trình mặt phẳng Oyz
a) Xác định điểm có thuộc mặt phẳng Oyz hay không
Để kiểm tra một điểm M(x₀; y₀; z₀) có thuộc mặt phẳng Oyz hay không, ta chỉ cần kiểm tra xem hoành độ của điểm đó có bằng 0 hay không. Nếu x₀ = 0, điểm M thuộc mặt phẳng Oyz; ngược lại, nếu x₀ ≠ 0, điểm M không thuộc mặt phẳng Oyz.
b) Viết phương trình mặt phẳng song song với mặt phẳng Oyz
Một mặt phẳng song song với mặt phẳng Oyz sẽ có dạng:
x = a
Trong đó, ‘a’ là một hằng số thực. Mặt phẳng này song song với Oyz và cách Oyz một khoảng |a|.
c) Tìm giao tuyến của mặt phẳng Oyz với các mặt phẳng khác
Để tìm giao tuyến của mặt phẳng Oyz (x = 0) với một mặt phẳng khác, ta giải hệ phương trình gồm phương trình của mặt phẳng Oyz và phương trình của mặt phẳng kia. Giao tuyến này thường là một đường thẳng nằm trên mặt phẳng Oyz.
d) Lập phương trình mặt phẳng đi qua một điểm và song song với mặt phẳng Oyz
Nếu một mặt phẳng đi qua điểm M(x₀; y₀; z₀) và song song với mặt phẳng Oyz, phương trình của nó sẽ là:
x = x₀
Hình ảnh minh họa phương trình tổng quát của mặt phẳng trong không gian Oxyz, giúp hình dung vị trí tương đối và các yếu tố xác định một mặt phẳng.
e) Tính khoảng cách từ một điểm đến mặt phẳng Oyz
Khoảng cách từ một điểm M(x₀; y₀; z₀) đến mặt phẳng Oyz được tính bằng trị tuyệt đối của hoành độ của điểm đó:
d(M, Oyz) = |x₀|
4. Ví dụ minh họa
Ví dụ 1: Cho điểm A(3; -2; 5). Tìm hình chiếu của A trên mặt phẳng Oyz.
Giải: Hình chiếu của A trên mặt phẳng Oyz là điểm A'(0; -2; 5).
Ví dụ 2: Viết phương trình mặt phẳng đi qua điểm B(-1; 4; 2) và song song với mặt phẳng Oyz.
Giải: Phương trình mặt phẳng cần tìm là x = -1.
5. Ứng dụng của phương trình mặt phẳng Oyz
- Trong hình học: Phương trình mặt phẳng Oyz được sử dụng để giải các bài toán liên quan đến vị trí tương đối giữa điểm, đường thẳng và mặt phẳng.
- Trong đồ họa máy tính: Mặt phẳng Oyz thường được sử dụng làm mặt phẳng tham chiếu để xây dựng các đối tượng 3D.
- Trong vật lý: Mặt phẳng Oyz có thể được sử dụng để mô tả các hệ tọa độ trong không gian, ví dụ như trong các bài toán về chuyển động của vật thể.
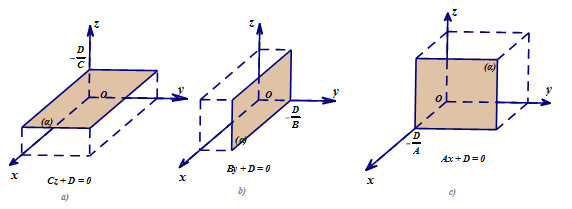
Hình ảnh minh họa các trường hợp đặc biệt của phương trình mặt phẳng khi các hệ số A, B, C bằng 0, liên hệ đến các trục tọa độ.
6. Tổng kết
Hiểu rõ về phương trình mặt phẳng Oyz là nền tảng quan trọng để nắm vững kiến thức về hình học giải tích không gian. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan và chi tiết về mặt phẳng Oyz, giúp bạn giải quyết các bài tập liên quan một cách hiệu quả. Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ giúp bạn củng cố kiến thức và áp dụng linh hoạt vào các bài toán thực tế.