Trong toán học, đặc biệt là lý thuyết tập hợp, khái niệm “Phần Bù Của A Trong B” đóng vai trò quan trọng. Bài viết này sẽ trình bày chi tiết về định nghĩa, ký hiệu, cách xác định và các ví dụ minh họa liên quan đến phần bù của A trong B.
Định Nghĩa và Ký Hiệu
Nếu A là một tập con của B ((A subset B)), thì hiệu của B và A ((B{rm{backslash }}A)) được gọi là phần bù của A trong B. Nói một cách đơn giản, phần bù của A trong B là tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A.
Ký hiệu của phần bù của A trong B là ({C_B}A). Như vậy, ta có:
({C_B}A = B{rm{backslash }}A = { x in B | x notin A } )
Biểu Diễn bằng Biểu Đồ Ven
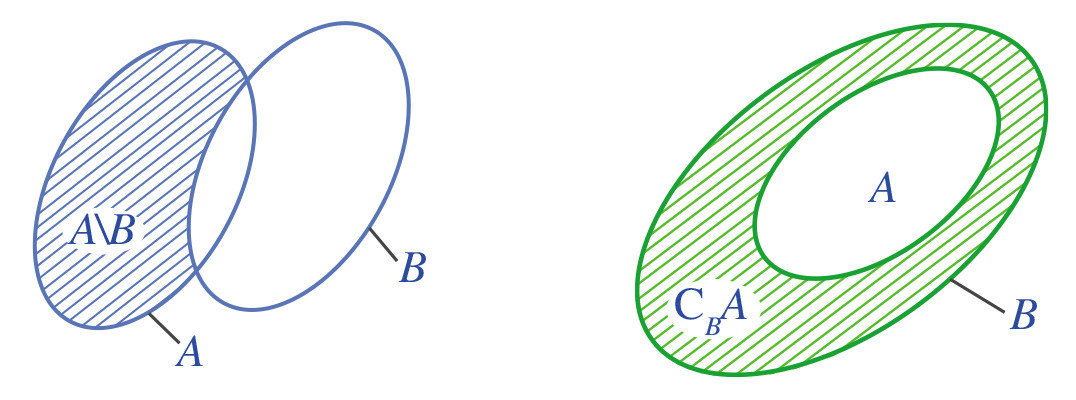
Biểu đồ Ven là một công cụ trực quan hữu ích để hiểu khái niệm phần bù. Phần bù của A trong B được biểu diễn bằng phần nằm trong tập B nhưng nằm ngoài tập A.
Ví dụ Minh Họa
Ví dụ 1:
Cho tập hợp (B = {1, 2, 3, 4, 5}) và tập hợp (A = {2, 4}). Vì (A subset B), ta có thể tìm phần bù của A trong B:
({C_B}A = B{rm{backslash }}A = {1, 3, 5})
Ví dụ 2:
Cho tập hợp số thực (mathbb{R}) và tập hợp (A = [0, 1]). Khi đó, phần bù của A trong (mathbb{R}) là:
({C_mathbb{R}}A = mathbb{R}{rm{backslash }}[0, 1] = ( – infty , 0) cup (1, + infty ))
Ứng Dụng của Phần Bù trong Giải Toán
Phần bù thường được sử dụng để giải các bài toán liên quan đến tập hợp, đặc biệt là các bài toán về tìm tập hợp thỏa mãn một điều kiện nào đó. Việc sử dụng phần bù có thể giúp đơn giản hóa bài toán và tìm ra lời giải một cách dễ dàng hơn. Ví dụ, khi muốn tìm các phần tử không thuộc một tập hợp con, ta có thể tìm phần bù của tập hợp con đó trong tập hợp lớn hơn.
Xác Định Hiệu của Hai Tập Hợp trên Trục Số
Khi làm việc với các tập hợp số, việc biểu diễn chúng trên trục số là một phương pháp hiệu quả để xác định hiệu của hai tập hợp và từ đó tìm ra phần bù nếu có.
Ví dụ 3:
Cho tập hợp (A = (-3; 5]) và (B = [1; +infty)). Xác định (A{rm{backslash }}B).
Dựa vào trục số, ta thấy:
(A{rm{backslash }}B = (-3; 1))
Phần bù của A giao B trong R
Tiếp tục ví dụ trên, xét phần bù của (A cap B) trong (mathbb{R}):
(A cap B = (-3; 5] cap [1; +infty) = [1; 5])
Vậy, ({C_mathbb{R}}(A cap B) = mathbb{R}{rm{backslash }}[1; 5] = (-infty; 1) cup (5; +infty))
Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về “phần bù của A trong B”, giúp bạn hiểu rõ hơn về khái niệm này và áp dụng nó vào giải các bài toán liên quan.