Trong toán học, đặc biệt là lý thuyết tập hợp, hiểu rõ về hiệu của hai tập hợp và Phần Bù là vô cùng quan trọng. Bài viết này sẽ đi sâu vào định nghĩa, ký hiệu, cách xác định và ví dụ minh họa về “phần bù” để bạn có cái nhìn toàn diện và ứng dụng hiệu quả.
1. Hiệu của hai tập hợp (A B)
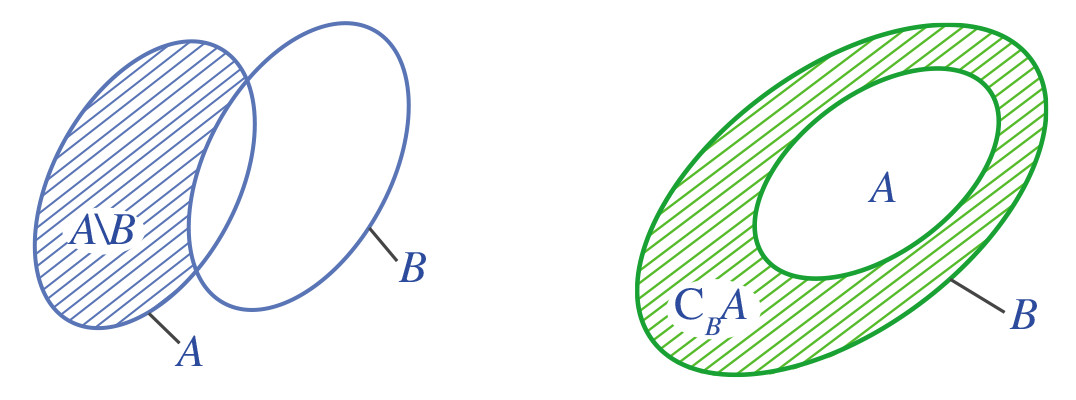
Hiệu của hai tập hợp A và B, ký hiệu là A B (hoặc A – B), là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B.
- Kí hiệu: A B
- Công thức: A B = { x | x ∈ A và x ∉ B }
2. Phần bù của một tập hợp (CBA)
Phần bù của tập hợp A trong tập hợp B, ký hiệu là CBA, là hiệu của B và A, với điều kiện A là tập con của B (A ⊆ B). Nói cách khác, phần bù của A trong B chứa tất cả các phần tử thuộc B nhưng không thuộc A. “Phần bù” là một trường hợp đặc biệt của phép hiệu.
- Kí hiệu: CBA
- Công thức: CBA = B A = { x | x ∈ B và x ∉ A }
Để dễ hình dung, bạn có thể xem biểu đồ Ven sau đây:
Alt text: Biểu đồ Ven minh họa phần bù của tập hợp A trong tập hợp B, vùng màu xám thể hiện các phần tử thuộc B nhưng không thuộc A, minh họa khái niệm phần bù.
3. Cách xác định hiệu và phần bù trên trục số
Để xác định hiệu của hai tập hợp A và B (hoặc phần bù nếu A là tập con của B) trên trục số, ta thực hiện các bước sau:
- Biểu diễn: Vẽ trục số và biểu diễn hai tập hợp A và B trên đó.
- Gạch bỏ: Gạch bỏ những phần của A mà thuộc B. Phần còn lại của A (không bị gạch) chính là hiệu A B.
Hình ảnh sau đây minh họa cách xác định hiệu trên trục số:
Alt text: Trục số biểu diễn hai tập hợp A và B, phần gạch chéo thể hiện các phần tử thuộc cả A và B, phần còn lại của A sau khi loại bỏ phần gạch chéo là hiệu của A và B.
4. Ví dụ minh họa
Ví dụ 1: Cho tập hợp C = {2; 3; 5; 7} và D = {-1; 3; 4; 5; 9}. Tìm C D.
- Giải: C D = {2; 7} (Các phần tử thuộc C nhưng không thuộc D).
Ví dụ 2: Cho tập hợp A = (-3; 5] và B = [1; +∞). Xác định A B và CR(A ∩ B).
-
Giải:
- A B = (-3; 1) (Các phần tử thuộc A nhưng không thuộc B).
- A ∩ B = (-3; 5] ∩ [1; +∞) = [1; 5]
- CR(A ∩ B) = R [1; 5] = (-∞; 1) ∪ (5; +∞) (Phần bù của giao giữa A và B trong tập số thực R).
5. Ứng dụng của phần bù
Khái niệm “phần bù” có nhiều ứng dụng quan trọng trong toán học và các lĩnh vực liên quan:
- Lý thuyết tập hợp: “Phần bù” giúp đơn giản hóa các phép toán tập hợp phức tạp, đặc biệt khi làm việc với các mệnh đề logic và chứng minh.
- Xác suất: Trong lý thuyết xác suất, “phần bù” của một sự kiện là tập hợp tất cả các kết quả không thuộc sự kiện đó. Việc tính xác suất của “phần bù” có thể đơn giản hơn so với tính trực tiếp xác suất của sự kiện ban đầu.
- Khoa học máy tính: “Phần bù” được sử dụng trong các thuật toán liên quan đến tìm kiếm, lọc dữ liệu và xử lý ảnh. Ví dụ, trong xử lý ảnh, “phần bù” của một vùng ảnh có thể được sử dụng để xác định các đối tượng hoặc đặc điểm quan trọng.
- Logic: “Phần bù” tương ứng với phép phủ định trong logic mệnh đề.
Hiểu rõ khái niệm “phần bù” và cách áp dụng nó sẽ giúp bạn giải quyết nhiều bài toán và vấn đề một cách hiệu quả hơn.