Khi nghiên cứu về chuyển động, hai khái niệm quan trọng cần phân biệt rõ ràng là độ dịch chuyển và quãng đường đi được. Mặc dù cả hai đều liên quan đến sự thay đổi vị trí của vật, nhưng chúng có ý nghĩa vật lý khác nhau.
I. Vị Trí và Thời Điểm
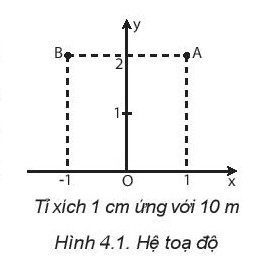
Để mô tả chuyển động của một vật, chúng ta cần xác định vị trí của nó tại các thời điểm khác nhau. Vị trí thường được xác định bằng hệ tọa độ vuông góc (Oxy) với gốc tọa độ là vị trí của vật mốc.
Ví dụ, trên hệ tọa độ Oxy, điểm A có tọa độ (10m; 20m) và điểm B có tọa độ (-10m; 20m).
Để xác định thời điểm, ta chọn một mốc thời gian và đo khoảng thời gian từ mốc đó đến thời điểm cần xác định. Hệ quy chiếu bao gồm hệ tọa độ, mốc thời gian và đồng hồ đo thời gian.
II. Độ Dịch Chuyển
Độ dịch chuyển là một đại lượng vectơ, được biểu diễn bằng một mũi tên nối vị trí đầu và vị trí cuối của chuyển động. Độ dài của mũi tên tỉ lệ với độ lớn của độ dịch chuyển, và hướng của mũi tên chỉ hướng từ vị trí đầu đến vị trí cuối.
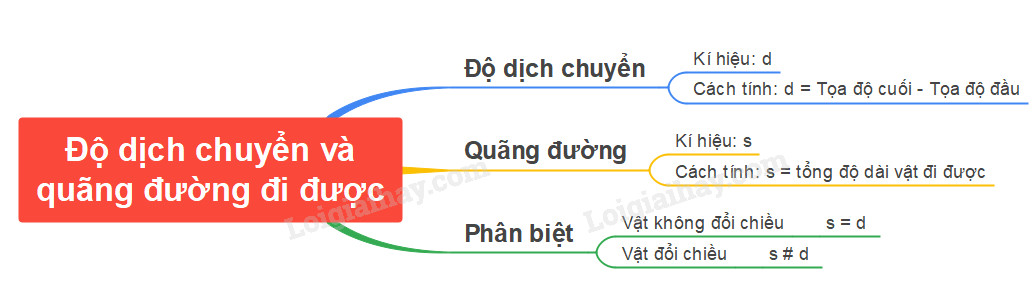
- Kí hiệu: (overline d )
- Đơn vị: mét (m)
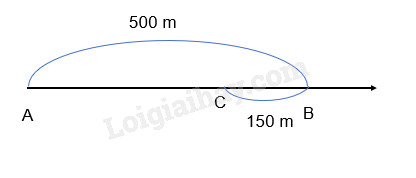
Ví dụ, nếu một vật di chuyển từ điểm A đến điểm B (500m) rồi quay lại điểm C (150m), độ dịch chuyển của vật là khoảng cách từ A đến C.
Trong ví dụ này, độ dịch chuyển là: (overline d = AC = 500 – 150 = 350(m))
III. Quãng Đường Đi Được
Quãng đường đi được là một đại lượng vô hướng, đo tổng độ dài mà vật đã di chuyển trong suốt quá trình chuyển động. Nó không quan tâm đến hướng di chuyển của vật.
Trong ví dụ trên, quãng đường đi được là tổng quãng đường từ A đến B cộng với quãng đường từ B đến C: s = AB + BC = 500 + 150 = 650 (m).
IV. So Sánh Độ Dịch Chuyển và Quãng Đường Đi Được
| Đặc điểm | Độ Dịch Chuyển | Quãng Đường Đi Được |
|---|---|---|
| Bản chất | Đại lượng vectơ | Đại lượng vô hướng |
| Định nghĩa | Khoảng cách từ điểm đầu đến điểm cuối | Tổng độ dài quỹ đạo chuyển động |
| Giá trị | Có thể âm, dương hoặc bằng không | Luôn dương hoặc bằng không |
| Phụ thuộc vào | Vị trí đầu và vị trí cuối | Toàn bộ đường đi của vật |
V. Trường Hợp Đặc Biệt
Độ dịch chuyển và quãng đường đi được có độ lớn bằng nhau khi vật chuyển động thẳng và không đổi chiều. Lúc này, quãng đường đi được chính là độ dài đoạn thẳng nối điểm đầu và điểm cuối.
VI. Tổng Hợp Độ Dịch Chuyển
Khi một vật thực hiện nhiều độ dịch chuyển liên tiếp, ta sử dụng phép cộng vectơ để tìm độ dịch chuyển tổng hợp.
VII. Ứng Dụng Thực Tế
Việc phân biệt rõ ràng độ dịch chuyển và quãng đường đi được rất quan trọng trong nhiều bài toán và ứng dụng thực tế, ví dụ như tính vận tốc trung bình và tốc độ trung bình của một vật. Vận tốc trung bình được tính dựa trên độ dịch chuyển, trong khi tốc độ trung bình được tính dựa trên quãng đường đi được.
Nắm vững sự khác biệt giữa độ dịch chuyển và quãng đường đi được sẽ giúp bạn hiểu sâu hơn về các khái niệm cơ bản trong động học và giải quyết các bài toán liên quan một cách chính xác.


