Parabol là một trong những đường conic quan trọng nhất trong toán học và có nhiều ứng dụng thực tế. Bài viết này sẽ đi sâu vào các khía cạnh khác nhau của “Parabol Có Dạng”, từ định nghĩa, phương trình, cách vẽ, đến sự tương quan giữa parabol và đường thẳng.
1. Định Nghĩa và Ứng Dụng Của Parabol
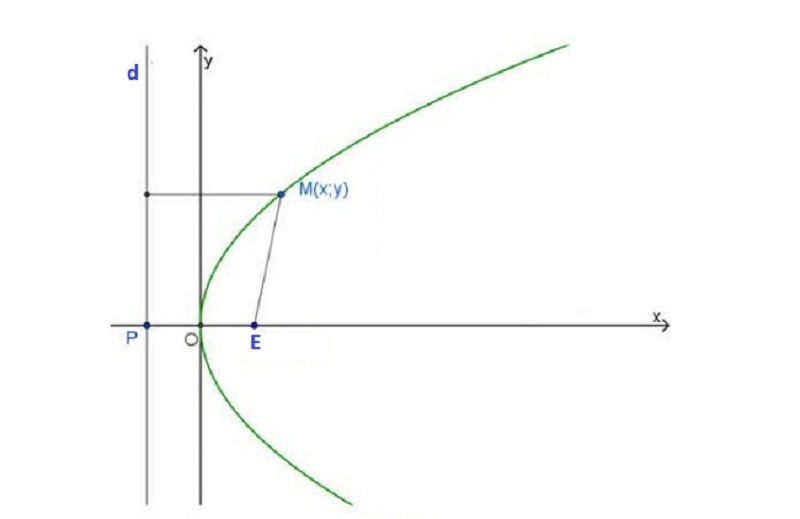
Parabol là một đường conic được tạo thành khi một mặt phẳng cắt một hình nón sao cho song song với một đường sinh của nón. Về mặt hình học, parabol là tập hợp các điểm cách đều một điểm cố định (tiêu điểm) và một đường thẳng cố định (đường chuẩn).
- Tiêu điểm (E): Điểm cố định.
- Đường chuẩn (d): Đường thẳng cố định không đi qua tiêu điểm.
- Tham số tiêu (p): Khoảng cách từ tiêu điểm đến đường chuẩn.
Parabol xuất hiện rất nhiều trong cuộc sống hàng ngày, từ kiến trúc đến công nghệ:
- Xây dựng cầu: Cầu có hình dạng parabol giúp phân bổ lực đều lên các trụ, tăng độ vững chắc.
- Thiết kế tàu lượn siêu tốc: Đường ray parabol tạo cảm giác mạnh và động lực cho tàu.
- Chế tạo mặt kính: Kính thiên văn phản xạ, đèn pin, đèn chiếu sáng sử dụng mặt cầu parabol để hội tụ ánh sáng.
- Anten parabol: Sử dụng để thu và phát sóng điện từ, ví dụ như anten vi sóng và chảo vệ tinh.
2. Phương Trình Đường Parabol
2.1. Phương Trình Tổng Quát
Phương trình tổng quát của parabol có dạng:
y = ax² + bx + c
Trong đó:
- a, b, c: Các hằng số, với a ≠ 0.
- Đỉnh parabol: Tọa độ đỉnh là (-b/2a, (b²-4ac)/4a)
- Hướng bề lõm: Nếu a > 0, bề lõm hướng lên; nếu a < 0, bề lõm hướng xuống.
2.2. Phương Trình Chính Tắc
Phương trình chính tắc của parabol có dạng đơn giản hơn:
y² = 2px (p > 0)
Trong đó:
- p: Tham số tiêu của parabol.
- Tiêu điểm: E(p/2; 0)
- Đường chuẩn: x = -p/2
3. Cách Vẽ Đường Cong Parabol
Có hai phương pháp chính để vẽ parabol: sử dụng compa và thước kẻ, hoặc dựa vào đồ thị hàm số bậc hai.
3.1. Vẽ Bằng Compa và Thước Kẻ
Các bước thực hiện:
- Xác định tiêu điểm E và đường chuẩn d.
- Kẻ đường thẳng vuông góc từ E đến d, gọi giao điểm là P.
- Chọn một điểm M’ bất kỳ trên đoạn PE.
- Kẻ đường thẳng song song với d đi qua M’.
- Dùng compa, vẽ một cung tròn tâm E, bán kính bằng khoảng cách từ O (trung điểm PE) đến M’. Giao điểm của cung tròn và đường thẳng song song là một điểm thuộc parabol.
- Lặp lại bước 3-5 với các điểm M’ khác nhau để tìm nhiều điểm thuộc parabol.
- Nối các điểm lại để được đường parabol.
3.2. Vẽ Bằng Đồ Thị Hàm Số Bậc Hai
Đồ thị của hàm số bậc hai y = ax² + bx + c là một parabol.
Các bước thực hiện:
- Xác định đỉnh parabol: (-b/2a; -Δ/4a), với Δ = b² – 4ac.
- Xác định trục đối xứng: x = -b/2a.
- Tìm giao điểm với trục tung: Điểm (0; c).
- Tìm giao điểm với trục hoành (nếu có): Giải phương trình
ax² + bx + c = 0. - Tìm thêm các điểm khác: Chọn các giá trị x khác nhau và tính giá trị y tương ứng. Lưu ý tính đối xứng của parabol.
- Vẽ parabol: Nối các điểm đã xác định, chú ý đến hình dạng và bề lõm của parabol (phụ thuộc vào dấu của a).
Ví dụ: Vẽ đồ thị hàm số y = -x² + 4x - 4
- Đỉnh: I(2; 0)
- Trục đối xứng: x = 2
- Giao điểm với trục tung: (0; -4)
- Giao điểm với trục hoành: (2; 0)
- Điểm đối xứng với (0; -4) qua x = 2: (4; -4)
- Vẽ parabol đi qua các điểm này.
4. Tương Quan Giữa Parabol và Đường Thẳng
Xét đường thẳng d: y = mx + n và parabol (P): y = ax² (a ≠ 0). Số giao điểm của chúng là số nghiệm của phương trình hoành độ giao điểm:
ax² = mx + n ⇔ ax² - mx - n = 0
- Δ > 0: d cắt (P) tại hai điểm phân biệt.
- Δ = 0: d tiếp xúc với (P).
- Δ < 0: d không cắt (P).
4.1. Phương Pháp Giải Bài Toán Tọa Độ Giao Điểm
- Viết phương trình hoành độ giao điểm.
- Giải phương trình bậc hai để tìm hoành độ giao điểm (x).
- Thay x vào phương trình của đường thẳng hoặc parabol để tìm tung độ giao điểm (y).
- Kết luận tọa độ giao điểm (x; y).
4.2. Các Dạng Bài Tập Thường Gặp
- Xác định số giao điểm: Dựa vào dấu của Δ.
- Tìm tọa độ giao điểm: Giải phương trình hoành độ giao điểm.
- Xác định tham số m để thỏa mãn điều kiện cho trước: Ví dụ, đường thẳng cắt parabol tại hai điểm nằm bên trái/phải trục tung, hoặc thỏa mãn một biểu thức nào đó liên quan đến tọa độ giao điểm.
- Bài toán liên quan đến diện tích: Tính diện tích tam giác, hình thang tạo bởi các giao điểm và các điểm khác trên đồ thị.
Ví dụ: Tìm tọa độ giao điểm của parabol y = x² và đường thẳng y = 2x - 1.
Giải:
x² = 2x - 1 ⇔ x² - 2x + 1 = 0 ⇔ (x - 1)² = 0 ⇔ x = 1
Với x = 1, ta có y = 1² = 1. Vậy tọa độ giao điểm là (1; 1).
Bài viết này đã trình bày một cách chi tiết về “parabol có dạng”, bao gồm định nghĩa, phương trình, cách vẽ và các bài toán liên quan. Hy vọng nó sẽ giúp bạn hiểu rõ hơn về đường conic quan trọng này.