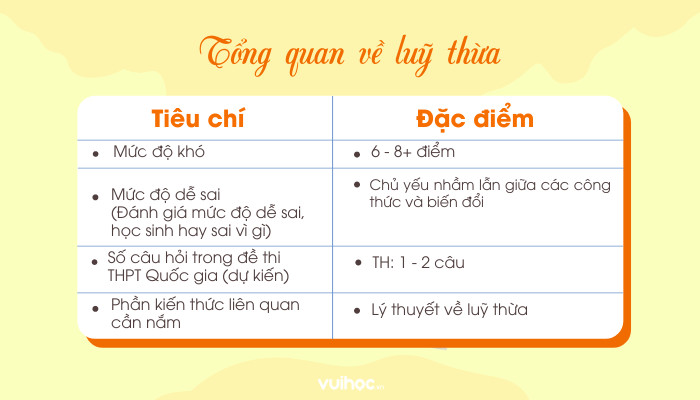
Lũy thừa là một khái niệm toán học quan trọng, đặc biệt khi xét đến “Nhân Lũy Thừa Cùng Số Mũ”. Bài viết này sẽ cung cấp kiến thức toàn diện và sâu sắc về chủ đề này, giúp bạn nắm vững các công thức và ứng dụng của nó.
1. Tổng Quan Về Lũy Thừa
1.1. Định Nghĩa Lũy Thừa
Lũy thừa là phép toán thực hiện trên hai số a và b, ký hiệu là $a^b$, đọc là “a mũ b” hoặc “lũy thừa bậc b của a”. Trong đó, a là cơ số và b là số mũ. Lũy thừa biểu thị phép nhân lặp đi lặp lại của cơ số a với chính nó b lần.
1.2. Phân Loại Lũy Thừa
Trong chương trình THPT, ta thường gặp ba dạng lũy thừa chính:
- Lũy thừa với số mũ nguyên: Số mũ là số nguyên.
- Lũy thừa với số mũ hữu tỉ: Số mũ là số hữu tỉ.
- Lũy thừa với số mũ thực: Số mũ là số thực.
Mỗi loại lũy thừa có những tính chất và quy tắc riêng, cần nắm vững để giải quyết bài tập.
1.2.1. Lũy thừa với số mũ nguyên
Cho $n$ là một số nguyên dương. Với $a$ là một số thực tùy ý, lũy thừa bậc $n$ của $a$ là tích của n thừa số $a$. Ta có công thức tổng quát như sau:
$a^n = a.a.a.a…a$ ($n$ thừa số $a$)
Với $a^0$ thì $a^0 = 1, a^{-n} = frac{1}{a^n}$
Lưu ý:
- $0^n$ và $0^{-n}$ không có nghĩa
- Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
1.2.2. Lũy thừa với số mũ hữu tỉ
Cho số thực $a$ dương và số hữu tỉ $r = frac{m}{n}$, trong đó $m in mathbb{Z}, n in mathbb{N}, n geq 2$.
Lũy thừa của số $a$ với số mũ $r$ là số $a^r$ xác định bởi: $a^r = a^{frac{m}{n}} = sqrt[n]{a^m}$
Đặc biệt: Khi $m = 1: a^{frac{1}{n}} = sqrt[n]{a}$
Ví dụ:
1.2.3. Lũy thừa với số mũ thực
Cho $a>0, a in mathbb{R}$, là một số vô tỉ, khi đó $a^alpha = lim{n rightarrow +infty }a(r^n)$ với $r^n$ là dãy số hữu tỉ thỏa mãn $lim{n rightarrow +infty }r^n = alpha $
Tính chất của lũy thừa với số mũ thực:
Cho a,b > 0; x,y $in$ R ta sẽ có:
-
$a^x.a^y = a^{x + y}$
-
$a^x : a^y = a^{x – y}$
-
$(a^x)^y = a^{x.y}$
-
$(ab)^x = a^xb^x$
-
$a^x = a^y Leftrightarrow x = y (a neq 1)$
-
Với a > 1 thì $a^x > a^y Leftrightarrow x > y$, với 0 < a < 1 thì $a^x > a^y Leftrightarrow x < y$
-
Với 0 < a < b thì $a^m < b^m$, nếu m là số nguyên âm thì $a^m > b^m$
1.3. Tính Chất và Công Thức Lũy Thừa Cơ Bản
Nắm vững các tính chất và công thức lũy thừa là chìa khóa để giải quyết các bài toán liên quan đến lũy thừa, đặc biệt là các bài toán về “nhân lũy thừa cùng số mũ”.
Tính chất về đẳng thức: Cho a ≠ 0; b ≠ 0; m, n ∈ R, ta có:
a) $a^m.a^n = a^{m+n}$
b)
c)
d) $(a.b)^m = a^m . b^m$
e)
Tính chất về bất đẳng thức:
So sánh cùng cơ số: Cho m, n ∈ R. Khi đó:
-
Với $a>1$ thì $a^m>a^nRightarrow m>n$
-
Với $0So sánh cùng số mũ:
-
Với số mũ dương $n>0: a>b>0Rightarrow a^n>b^n$
-
Với số mũ âm $nb>0Rightarrow a^n
Ngoài ra còn có một số công thức khác trong các trường hợp đặc biệt, cụ thể như sau:
- Lũy thừa của số e:
Số $e$ là hằng số toán học quan trọng, xấp xỉ 2.718 và là cơ số của logarit tự nhiên. Số $e$ được định nghĩa qua giới hạn sau:
Hàm $e$ mũ, được định nghĩa bởi $e=lim_{xrightarrow infty }(1+frac{1}{n})^n$ ở đây $x$ được viết như số mũ vì nó thỏa mãn đẳng thức cơ bản của lũy thừa $e^{x+y}=e^x.e^y$
Hàm $e$ mũ xác định với tất cả các giá trị nguyên, hữu tỷ, thực và cả giá trị phức của $x$.
Có thể chứng minh ngắn gọn rằng hàm $e$ mũ với $x$ là số nguyên dương k chính là $e^k$ như sau:
Chứng minh này cũng chứng tỏ rằng $e^{x+y}$ thỏa mãn đẳng thức lũy thừa khi x và y là các số nguyên dương. Kết quả này cũng có thể mở rộng cho tất cả các số không phải là số nguyên dương.
- Hàm lũy thừa với số mũ thực:
Lũy thừa với số mũ thực cũng thường được định nghĩa bằng cách sử dụng logarit thay cho sử dụng giới hạn của các số hữu tỷ.
Logarit tự nhiên $ln(x)$ là hàm ngược của hàm $e^x$. Theo đó $lnx$ là số $b$ sao cho $x=e^b$
Nếu $a$ là số thực dương, $x$ là số thực bất kỳ ta có $a=elna$ nên nếu ax được định nghĩa nhờ hàm logarit tự nhiên thì ta cần phải có:
$a^x=(e^{lna})^x=e^{x.lna}$
Điều này dẫn tới định nghĩa $a^x=e^{x.lna}$ với mọi số thực $x$ và số thực dương $a$
2. Lũy Thừa Cùng Số Mũ
2.1. Định Nghĩa
“Nhân lũy thừa cùng số mũ” là phép toán nhân hai hay nhiều lũy thừa có cùng số mũ nhưng cơ số khác nhau.
2.2. Công Thức Nhân Lũy Thừa Cùng Số Mũ
Công thức tổng quát để nhân lũy thừa cùng số mũ:
$a^n.b^n = (a.b)^n$
Công thức này có thể mở rộng cho nhiều lũy thừa hơn:
$a^n.b^n.c^n = (a.b.c)^n$
Ví dụ:
- $2^3 . 5^3 = (2.5)^3 = 10^3 = 1000$
- $3^2 . 4^2 . (frac{1}{2})^2 = (3.4.frac{1}{2})^2 = 6^2 = 36$
2.3. Ứng Dụng của Nhân Lũy Thừa Cùng Số Mũ
Nhân lũy thừa cùng số mũ được ứng dụng rộng rãi trong các bài toán đại số, giải phương trình, đơn giản biểu thức và tính toán. Việc nắm vững công thức này giúp giải quyết bài toán nhanh chóng và chính xác.
3. Bài Tập Vận Dụng
Để củng cố kiến thức, hãy luyện tập các bài tập sau:
- Tính: $2^5 . 5^5$
- Rút gọn biểu thức: $x^3 . y^3 . z^3$
- Giải phương trình: $4^x . 9^x = 36$
Hy vọng bài viết này đã cung cấp cho bạn kiến thức đầy đủ và chi tiết về “nhân lũy thừa cùng số mũ”. Hãy luyện tập thường xuyên để nắm vững và áp dụng thành thạo công thức này trong giải toán.