Nguyên hàm của ln(x) là một chủ đề quan trọng trong giải tích, đặc biệt trong chương trình Toán lớp 12 và các kỳ thi quan trọng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về nguyên hàm của ln(x), bao gồm công thức, phương pháp tính và các ví dụ minh họa chi tiết, giúp bạn nắm vững kiến thức và tự tin giải quyết các bài tập liên quan.
1. Khái Niệm Nguyên Hàm của ln(x)
Cho hàm số $f(x)$ xác định trên khoảng K. Hàm số $F(x)$ được gọi là nguyên hàm của $f(x)$ trên K nếu $F'(x) = f(x)$ với mọi $x in K$.
Để tìm nguyên hàm của $ln(x)$, ta sử dụng phương pháp tích phân từng phần:
Đặt $begin{cases} u = ln(x) dv = dx end{cases} Rightarrow begin{cases} du = frac{1}{x} dx v = x end{cases}$
Khi đó:
$int ln(x) dx = xln(x) – int x cdot frac{1}{x} dx = xln(x) – int dx = xln(x) – x + C$
Vậy, nguyên hàm của $ln(x)$ là $xln(x) – x + C$, trong đó C là hằng số tích phân.
2. Bảng Công Thức Nguyên Hàm Liên Quan đến ln(x)
Bảng dưới đây tổng hợp công thức nguyên hàm của $ln(x)$ và một số nguyên hàm cơ bản thường gặp khác:
3. Các Phương Pháp Tính Nguyên Hàm của ln(x)
3.1. Nguyên Hàm của ln(x+1)
Để tính nguyên hàm của $ln(x+1)$, ta sử dụng phương pháp tích phân từng phần tương tự như trên.
Ví dụ 1: Tính $int_{1}^{2} ln(x+1) dx$, biết kết quả có dạng $aln(3) + bln(2) + c$, với a, b, c là các số nguyên. Tính $S = a + b + c$.
Giải:
Đặt $begin{cases} u = ln(x+1) dv = dx end{cases} Rightarrow begin{cases} du = frac{1}{x+1} dx v = x+1 end{cases}$
Khi đó:
$int{1}^{2} ln(x+1) dx = (x+1)ln(x+1) Big|{1}^{2} – int_{1}^{2} dx = 3ln(3) – 2ln(2) – (2-1) = 3ln(3) – 2ln(2) – 1$
Vậy $a = 3, b = -2, c = -1$ và $S = a + b + c = 3 – 2 – 1 = 0$.
Ví dụ 2: Tìm nguyên hàm của hàm số $B = int x^2 ln(x) dx$
Giải:
$B = int x^2 ln(x) dx = int ln(x) d(frac{x^3}{3}) = frac{x^3}{3}ln(x) – int frac{x^3}{3} d(ln(x)) = frac{x^3}{3}ln(x) – int frac{x^3}{3} cdot frac{1}{x} dx = frac{x^3}{3}ln(x) – frac{1}{3} int x^2 dx = frac{x^3}{3}ln(x) – frac{x^3}{9} + C$
3.2. Nguyên Hàm của (1+ln(x))/x
Ví dụ 1: Tìm nguyên hàm $J = int frac{(ln(x)+1)ln(x)}{x(frac{ln(x)+1}{x}+1)^3} dx$
Giải:
$J = int frac{ln(x)+1}{x(frac{ln(x)+1}{x}+1)^3} cdot frac{ln(x)}{x^2} dx$
Đặt $t = frac{ln(x)+1}{x} Rightarrow dt = frac{x cdot frac{1}{x} – (ln(x)+1)}{x^2} dx = frac{-ln(x)}{x^2}dx Rightarrow -dt= frac{ln(x)}{x^2}dx$
Khi đó $J= – int frac{tdt}{(t+1)^3} = – int [frac{1}{(t+1)^2}-frac{1}{(t+1)^3}]dt= frac{1}{t+1} – frac{1}{2(t+1)^2} + C = frac{x}{lnx+x+1} – frac{x^{2}}{2(lnx+1+x^{2})} + C$
Ví dụ 2: Tìm nguyên hàm của:
a) $int x cdot 2^x dx$
b) $int (x^2-1) e^x dx$
Giải:
a) Đặt $begin{cases} u = x dv = 2^x dx end{cases} Rightarrow begin{cases} du = dx v = frac{2^x}{ln(2)} end{cases}$
Khi đó: $int x 2^x dx = frac{x cdot 2^x}{ln(2)} – int frac{2^x}{ln(2)} dx = frac{x cdot 2^x}{ln(2)} – frac{2^x}{ln^2(2)} + C$
b) Đặt $begin{cases} u = x^2 – 1 dv = e^x dx end{cases} Rightarrow begin{cases} du = 2x dx v = e^x end{cases}$
Suy ra $int (x^2 – 1)e^x dx = (x^2 – 1)e^x – int 2x e^x dx$
Đặt $begin{cases} u = 2x dv = e^x dx end{cases} Rightarrow begin{cases} du = 2 dx v = e^x end{cases}$
Khi đó $int (x^2-1) e^x dx = (x^2 – 1)e^x – (2x e^x – int 2 e^x dx) = (x^2 – 1)e^x – 2x e^x + 2e^x + C = e^x(x^2 – 2x + 1) + C$
Ví dụ 3: Tìm tất cả các nguyên hàm của hàm số $f(x) = (3x^2 + 1)ln(x)$
Giải:
Đặt $begin{cases} u = ln(x) dv = (3x^2 + 1) dx end{cases} Rightarrow begin{cases} du = frac{1}{x} dx v = int (3x^2 + 1) dx = x^3 + x end{cases}$
$Rightarrow I = (x^3 + x)ln(x) – int (x^3 + x) cdot frac{1}{x} dx = x(x^2 + 1)ln(x) – int (x^2 + 1) dx = x(x^2 + 1)ln(x) – frac{x^3}{3} – x + C$
3.3. Nguyên Hàm của ln(ax+b)
Ví dụ 1: Giải bất phương trình $ln(2x^2 + 3) > ln(x^2 + ax + 1)$ nghiệm đúng với mọi số thực x.
Giải:
Ví dụ 2: Tính nguyên hàm:
a) $int 2x ln(x-1) dx$
b) $int frac{ln(x+1)}{x^2} dx$
Giải:
a) Đặt $begin{cases} u = ln(x-1) dv = 2x dx end{cases} Rightarrow begin{cases} du = frac{1}{x-1} dx v = x^2 end{cases}$
Khi đó $int 2x ln(x-1) dx = x^2ln(x-1) – int frac{x^2}{x-1} dx = x^2ln(x-1) – int (x+1 + frac{1}{x-1}) dx= x^2ln(x-1) – frac{x^2}{2} – x – ln|x-1|+C$
b) Đặt $begin{cases} u = ln(x+1) dv = frac{1}{x^2} dx end{cases} Rightarrow begin{cases} du = frac{1}{x+1} dx v = -frac{1}{x} end{cases}$
$Rightarrow F(x) = -frac{1}{x}ln(x+1) + int frac{1}{x(x+1)} dx = -frac{1}{x}ln(x+1) + int (frac{1}{x} – frac{1}{x+1}) dx= -frac{1}{x}ln(x+1) + ln|x| – ln|x+1|+C$
3.4. Nguyên Hàm của ln(x^2+1)dx
Ví dụ 1: Tìm nguyên hàm $I = int x ln(x^2 + 1) dx$
Giải:
Ví dụ 2: Cho $int_{1}^{2} frac{ln(1+x)}{x^2} dx = aln(2) + bln(3)$, với a và b là các số hữu tỉ. Tính P = ab.
Giải:
Đặt $begin{cases} u = ln(1+x) dv = frac{1}{x^2} dx end{cases} Rightarrow begin{cases} du = frac{1}{1+x} dx v = -frac{1}{x} end{cases}$
Khi đó $I = -frac{1}{x}ln(1+x) Big|{1}^{2} + int{1}^{2} frac{1}{x(1+x)} dx = -frac{1}{2}ln(3) + ln(2) + int{1}^{2} (frac{1}{x} – frac{1}{1+x}) dx = -frac{1}{2}ln(3) + ln(2) + (ln|x| – ln|x+1|) Big|{1}^{2}= -frac{1}{2}ln(3) + ln(2) + ln(frac{2}{3}) – ln(frac{1}{2})= -frac{1}{2}ln(3) + ln(2) + ln(2) – ln(3) + ln(2) = 3ln(2) – frac{3}{2}ln(3)$
Suy ra $a = 3, b = -frac{3}{2}$. Vậy $P = ab = 3 cdot (-frac{3}{2}) = -frac{9}{2}$
3.5. Nguyên Hàm của Hàm Số f(x) = ln(x)/x
Ví dụ 1: Tính đạo hàm của hàm số $f(x) = frac{1}{x} + frac{ln(x)}{x}$
Giải:
$y’ = -frac{1}{x^2} + frac{frac{1}{x} cdot x – ln(x)}{x^2} = -frac{1}{x^2} + frac{1 – ln(x)}{x^2} = -frac{ln(x)}{x^2}$
Ví dụ 2: Giả sử tích phân $I = int_{1}^{5} frac{1}{1 + sqrt{3x+1}} dx = a + bln(3) + cln(5)$. Tính $a + b + c$.
Giải:
Đặt $t = sqrt{3x+1} Rightarrow t^2 = 3x + 1 Rightarrow 2tdt = 3dx Rightarrow dx = frac{2}{3}tdt$
Đổi cận:
| x | 1 | 5 |
|---|---|---|
| t | 2 | 4 |

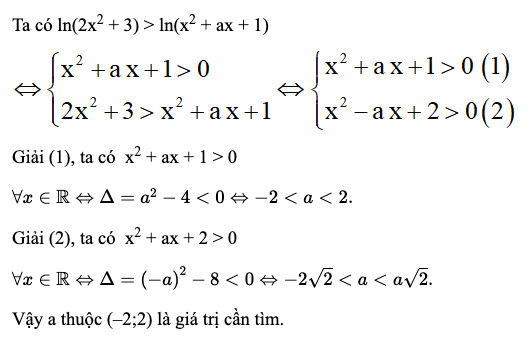
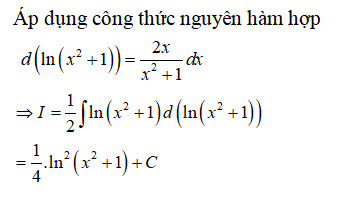
Khi đó $I = int{2}^{4} frac{1}{1+t} cdot frac{2}{3} t dt = frac{2}{3} int{2}^{4} frac{t}{t+1} dt = frac{2}{3} int{2}^{4} (1 – frac{1}{t+1}) dt = frac{2}{3} (t – ln|t+1|) Big|{2}^{4} = frac{2}{3} (4 – ln(5) – 2 + ln(3)) = frac{4}{3} + frac{2}{3}ln(3) – frac{2}{3}ln(5)$
Do đó $a = frac{4}{3}; b = frac{2}{3}; c = -frac{2}{3}$
Vậy $a + b + c = frac{4}{3}$
Ví dụ 3: Biết tích phân $int_{0}^{ln(6)} frac{e^x}{1 + sqrt{e^x + 3}} dx = a + bln(2) + cln(3)$, với a, b, c là các số nguyên. Tính T = a + b + c.
Giải:
Đặt $t = sqrt{e^x + 3} Rightarrow t^2 = e^x + 3 Rightarrow 2tdt = e^x dx$
Đổi cận: $begin{cases} x = ln(6) x = 0 end{cases} Rightarrow begin{cases} t = 3 t = 2 end{cases}$
Suy ra $int{0}^{ln(6)} frac{e^x}{1 + sqrt{e^x + 3}} dx = int{2}^{3} frac{2t}{1+t} dt = 2int{2}^{3} (1 – frac{1}{1+t}) dt = 2(t – ln|t+1|) Big|{2}^{3} = 2(3 – ln(4) – 2 + ln(3)) = 2 – 4ln(2) + 2ln(3)$
$Rightarrow begin{cases} a = 2 b = -4 c = 2 end{cases}$
Vậy T = a + b + c = 0
3.6. Tính Nguyên Hàm của ln(ln(x))/x
Ví dụ 1: Tính nguyên hàm của hàm số $I = int frac{ln(ln(x))}{x} dx$
Giải:
Đặt $ln(x) = t Rightarrow dt = frac{dx}{x}$
Suy ra $I = int frac{ln(ln(x))}{x} dx = int ln(t) dt$
Đặt $begin{cases} u = ln(t) dv = dt end{cases} Rightarrow begin{cases} du = frac{dt}{t} v = t end{cases}$
Theo công thức tính nguyên hàm từng phần, ta có:
$I = tln(t) – int dt = tln(t) – t + C = ln(x)ln(ln(x)) – ln(x) + C$
Ví dụ 2: Cho $I = int_{1}^{e} frac{ln(x)}{x(ln(x)+2)^2} dx = aln(3) + bln(2) + frac{c}{3}$ với a, b, c $in Z$. Khẳng định nào sau đây đúng.
Giải:
Đặt $ln(x) + 2 = t Rightarrow frac{dx}{x} = dt$
Đổi cận:
x = 1 -> t = 2
x = e -> t = 3
$I = int{2}^{3} frac{t-2}{t^2} dt = int{2}^{3} frac{1}{t} dt – 2int{2}^{3} frac{1}{t^2} dt = ln(t)Big|{2}^{3} + frac{2}{t}Big|_{2}^{3} = ln(3) – ln(2) + frac{2}{3} – 1 = ln(3) – ln(2) – frac{1}{3}$
=> a = 1; b = -1; c = -1
Vậy $a^2 + b^2 + c^2 = 3$
Hy vọng với những kiến thức và ví dụ minh họa chi tiết trên, bạn đã nắm vững cách tính nguyên hàm của ln(x) và có thể áp dụng vào giải các bài tập liên quan. Chúc bạn học tốt!