Bài viết này sẽ cung cấp một cái nhìn toàn diện về nguyên hàm của hàm số ln(2x+1), bao gồm công thức, phương pháp tính toán chi tiết và các ứng dụng thực tế.
Để tìm Nguyên Hàm Của Ln(2x+1), chúng ta sẽ sử dụng phương pháp tích phân từng phần. Đây là một kỹ thuật quan trọng trong giải tích, giúp chúng ta xử lý các tích phân phức tạp bằng cách chuyển đổi chúng thành các dạng đơn giản hơn.
Công thức tích phân từng phần có dạng:
∫u dv = uv – ∫v du
Trong trường hợp này, ta chọn:
- u = ln(2x+1)
- dv = dx
Khi đó:
- du = 2/(2x+1) dx
- v = x
Áp dụng công thức tích phân từng phần, ta có:
∫ln(2x+1) dx = xln(2x+1) – ∫x * [2/(2x+1)] dx
Bây giờ, chúng ta cần tính tích phân ∫[2x/(2x+1)] dx. Để làm điều này, ta có thể viết lại biểu thức dưới dạng:
2x/(2x+1) = 1 – 1/(2x+1)
Do đó:
∫[2x/(2x+1)] dx = ∫[1 – 1/(2x+1)] dx = x – (1/2)ln|2x+1| + C
Thay kết quả này trở lại biểu thức ban đầu, ta được:
∫ln(2x+1) dx = xln(2x+1) – [x – (1/2)ln|2x+1|] + C
= xln(2x+1) – x + (1/2)ln|2x+1| + C
Vậy, nguyên hàm của ln(2x+1) là:
F(x) = xln(2x+1) – x + (1/2)ln|2x+1| + C
Trong đó C là hằng số tích phân.
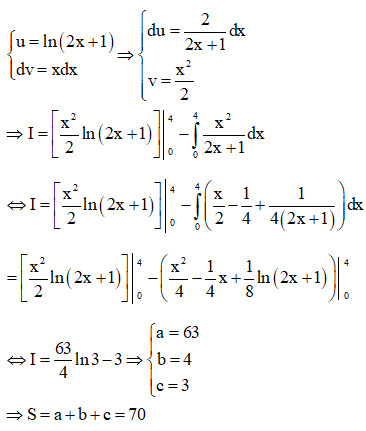Công thức tính tích phân từng phần sử dụng trong bài toán nguyên hàm ln(2x+1)
Ngoài công thức tổng quát, việc hiểu rõ cách áp dụng vào các bài toán cụ thể là vô cùng quan trọng. Xét ví dụ sau:
Ví dụ: Tính tích phân xác định từ 0 đến 4 của xln(2x+1) dx.
Để giải quyết bài toán này, ta cần kết hợp phương pháp tích phân từng phần đã sử dụng để tìm nguyên hàm của ln(2x+1) và sau đó áp dụng giới hạn tích phân.
∫04xln(2x+1)dx
Sử dụng tích phân từng phần, đặt u = ln(2x+1) và dv = xdx, suy ra du = 2/(2x+1) dx và v = x²/2.
Áp dụng công thức tích phân từng phần:
∫04xln(2x+1)dx = [x²/2 ln(2x+1)]04 – ∫04 (x²/2) [2/(2x+1)] dx
= [8ln(9) – 0] – ∫04 x²/(2x+1) dx
Bây giờ, ta cần tính tích phân ∫04 x²/(2x+1) dx. Ta có thể thực hiện phép chia đa thức hoặc biến đổi đại số để đơn giản hóa biểu thức.
x²/(2x+1) = (1/2)x – 1/4 + 1/(4(2x+1))
Do đó:
∫04 x²/(2x+1) dx = ∫04 [(1/2)x – 1/4 + 1/(4(2x+1))] dx
= [(1/4)x² – (1/4)x + (1/8)ln|2x+1|]04
= [4 – 1 + (1/8)ln(9)] – [0 – 0 + (1/8)ln(1)]
= 3 + (1/8)ln(9)
Thay kết quả này trở lại biểu thức ban đầu:
∫04xln(2x+1)dx = 8ln(9) – [3 + (1/8)ln(9)]
= 8ln(9) – 3 – (1/8)ln(9)
= (63/8)ln(9) – 3
= (63/4)ln(3) – 3
So sánh với dạng abln3-c, ta có a = 63, b = 4, c = 3.
Vậy S = a+b+c = 63 + 4 + 3 = 70.
Nguyên hàm của ln(2x+1) không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau. Một số ví dụ bao gồm:
-
Tính toán diện tích và thể tích: Trong hình học, nguyên hàm có thể được sử dụng để tính diện tích của các hình phẳng giới hạn bởi đường cong và thể tích của các vật thể tròn xoay.
-
Giải các bài toán vật lý: Trong vật lý, nguyên hàm được sử dụng để tính quãng đường đi được của một vật thể khi biết vận tốc của nó theo thời gian, hoặc để tính công thực hiện bởi một lực biến thiên.
-
Ứng dụng trong kinh tế: Trong kinh tế, nguyên hàm có thể được sử dụng để tính tổng doanh thu khi biết hàm doanh thu biên, hoặc để tính tổng chi phí khi biết hàm chi phí biên.
Thông qua bài viết này, hy vọng bạn đã nắm vững công thức, phương pháp tính toán và các ứng dụng quan trọng của nguyên hàm ln(2x+1). Việc hiểu rõ và vận dụng thành thạo các kiến thức này sẽ giúp bạn giải quyết các bài toán tích phân một cách hiệu quả và tự tin hơn.
