Bài toán về sự nổ của một vật thể đang chuyển động, đặc biệt là Một Viên đạn Pháo đang Bay Ngang Với Vận Tốc 50m/s, là một ví dụ điển hình về ứng dụng định luật bảo toàn động lượng trong vật lý. Xét một viên đạn pháo có khối lượng tổng cộng là 5kg đang bay ngang với vận tốc ổn định, sau đó nổ thành hai mảnh với khối lượng khác nhau. Việc xác định vận tốc và hướng đi của từng mảnh sau khi nổ là một bài toán thú vị, đòi hỏi sự kết hợp giữa lý thuyết và kỹ năng giải toán.
Trong trường hợp này, viên đạn pháo đang bay ở độ cao 125m với vận tốc 50m/s. Ngay lập tức, nó nổ thành hai mảnh, một mảnh 2kg và một mảnh 3kg. Mảnh nhỏ hơn bay thẳng đứng xuống dưới và chạm đất với vận tốc 100m/s. Mục tiêu là tìm ra vận tốc và hướng đi của mảnh lớn hơn ngay sau vụ nổ.
Để giải quyết bài toán này, chúng ta cần áp dụng định luật bảo toàn động lượng. Định luật này nói rằng tổng động lượng của một hệ kín (trong trường hợp này là viên đạn pháo trước và sau khi nổ) là không đổi.
Động lượng ban đầu của viên đạn pháo là:
p = mv = (2kg + 3kg) * 50 m/s = 250 kg.m/sXét mảnh nhỏ (2kg) bay thẳng đứng xuống dưới. Vận tốc của mảnh nhỏ ngay trước khi chạm đất là 100m/s. Tuy nhiên, ta cần tìm vận tốc của nó ngay sau khi nổ. Ta có thể sử dụng công thức liên hệ giữa vận tốc và độ cao để tìm vận tốc ban đầu của mảnh nhỏ:
v1^2 = v0^2 + 2gh
Trong đó:
- v1 = 100m/s (vận tốc khi chạm đất)
- g = 10m/s^2 (gia tốc trọng trường)
- h = 125m (độ cao)
Từ đó suy ra vận tốc ban đầu của mảnh nhỏ ngay sau khi nổ (v0) là:
v0 = √(v1^2 – 2gh) = √(100^2 – 2 10 125) = √(10000 – 2500) = √7500 ≈ 86.6 m/s (hướng xuống)
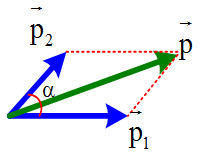Hình minh họa viên đạn pháo nổ trên không trung
Tiếp theo, áp dụng định luật bảo toàn động lượng:
p = p1 + p2
Trong đó:
- p là động lượng ban đầu của viên đạn pháo (250 kg.m/s)
- p1 là động lượng của mảnh nhỏ (2kg * 86.6 m/s hướng xuống)
- p2 là động lượng của mảnh lớn (3kg * v2, v2 là vận tốc cần tìm)
Vì động lượng là một đại lượng vector, ta cần phân tích thành các thành phần theo phương ngang và phương dọc. Ban đầu, viên đạn chỉ có động lượng theo phương ngang. Sau khi nổ, mảnh nhỏ chỉ có động lượng theo phương dọc (hướng xuống). Do đó, mảnh lớn phải có cả động lượng theo phương ngang và phương dọc để bảo toàn động lượng tổng cộng.
Từ định luật bảo toàn động lượng, ta có:
- Theo phương ngang: 250 = 0 + 3 * v2x (v2x là thành phần vận tốc theo phương ngang của mảnh lớn)
- Theo phương dọc: 0 = -2 86.6 + 3 v2y (v2y là thành phần vận tốc theo phương dọc của mảnh lớn)
Giải hệ phương trình trên, ta được:
- v2x = 250 / 3 ≈ 83.3 m/s
- v2y = (2 * 86.6) / 3 ≈ 57.7 m/s
Vậy, vận tốc của mảnh lớn ngay sau khi nổ là:
v2 = √(v2x^2 + v2y^2) = √((83.3)^2 + (57.7)^2) ≈ √(6938.89 + 3329.29) ≈ √10268.18 ≈ 101.3 m/s
Hướng của vận tốc mảnh lớn có thể được xác định bằng góc α so với phương ngang:
tan(α) = v2y / v2x = 57.7 / 83.3 ≈ 0.692
α = arctan(0.692) ≈ 34.7°
Do đó, mảnh lớn (3kg) bay với vận tốc khoảng 101.3 m/s theo hướng nghiêng lên trên một góc khoảng 34.7° so với phương ngang.
Phân tích trên cho thấy, một viên đạn pháo đang bay ngang với vận tốc 50m/s khi nổ sẽ tạo ra các mảnh văng theo nhiều hướng khác nhau, phụ thuộc vào khối lượng và động lượng của từng mảnh. Việc hiểu rõ các định luật vật lý như bảo toàn động lượng là rất quan trọng trong việc giải quyết các bài toán liên quan đến chuyển động và va chạm.
