I. Định Nghĩa Chuyển Động Tròn Đều
1. Chuyển động tròn: Là loại chuyển động mà quỹ đạo của vật là một đường tròn. Đây là một dạng chuyển động hai chiều phổ biến trong tự nhiên và kỹ thuật.
2. Chuyển động tròn đều: Là một trường hợp đặc biệt của chuyển động tròn, trong đó vật di chuyển trên đường tròn và đi được những cung tròn có độ dài bằng nhau trong những khoảng thời gian bằng nhau bất kỳ. Điều này có nghĩa là tốc độ góc của vật là không đổi.
II. Các Đại Lượng Đặc Trưng Cho Chuyển Động Tròn Đều
1. Vận Tốc Dài (v)
Vận tốc dài, còn gọi là tốc độ dài, là độ dài cung tròn mà vật đi được trong một đơn vị thời gian.
Công thức: (v = frac{{Delta s}}{{Delta t}})
Trong chuyển động tròn đều, độ lớn của vận tốc dài là không đổi, nhưng hướng của vận tốc luôn thay đổi (tiếp tuyến với đường tròn tại điểm đang xét).
2. Tốc Độ Góc (ω)
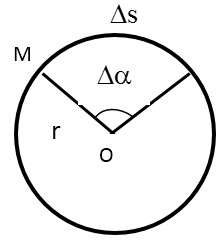
Tốc độ góc là đại lượng đo bằng góc mà bán kính nối từ tâm đường tròn đến vật quét được trong một đơn vị thời gian.
Alt: Hình ảnh minh họa góc quét Δα trong chuyển động tròn đều với bán kính R.
Công thức: (omega= dfrac{Delta alpha }{Delta t})
Trong đó:
- (∆α) là góc (tính bằng radian) mà bán kính quét được trong thời gian (∆t).
- Đơn vị của tốc độ góc là radian trên giây (rad/s).
Tốc độ góc là một đại lượng quan trọng, cho biết mức độ nhanh chậm của chuyển động tròn.
3. Chu Kỳ (T)
Chu kỳ của chuyển động tròn đều là thời gian để vật đi hết một vòng tròn.
Công thức: (T =dfrac{2pi }{omega })
Đơn vị của chu kỳ là giây (s).
4. Tần Số (f)
Tần số của chuyển động tròn đều là số vòng mà vật đi được trong một giây.
Công thức: (f=dfrac{1}{T})
Đơn vị của tần số là vòng trên giây (vòng/s) hoặc Hertz (Hz).
5. Mối Liên Hệ Giữa Vận Tốc Dài và Tốc Độ Góc
Vận tốc dài và tốc độ góc liên hệ với nhau qua bán kính quỹ đạo:
(v = ω.r)
Trong đó:
- v là vận tốc dài (m/s)
- ω là tốc độ góc (rad/s)
- r là bán kính quỹ đạo (m)
III. Gia Tốc Hướng Tâm
Trong chuyển động tròn đều, mặc dù tốc độ (độ lớn vận tốc) không đổi, nhưng vận tốc luôn thay đổi về hướng. Sự thay đổi hướng của vận tốc gây ra gia tốc, gọi là gia tốc hướng tâm.
Gia tốc hướng tâm luôn hướng vào tâm của quỹ đạo tròn.
Công thức: ( a_{ht}=dfrac{v^{^{2}}}{r}=r{omega}^2)
Trong đó:
- (a_{ht}) là gia tốc hướng tâm (m/s²)
- v là vận tốc dài (m/s)
- ω là tốc độ góc (rad/s)
- r là bán kính quỹ đạo (m)
IV. Ứng Dụng của Chuyển Động Tròn Đều
Chuyển động tròn đều có rất nhiều ứng dụng trong thực tế, ví dụ:
-
Vệ tinh nhân tạo: Vệ tinh quay quanh Trái Đất có thể coi là chuyển động tròn đều (hoặc gần đúng là tròn đều).
-
Chuyển động của các hành tinh quanh Mặt Trời: Mặc dù quỹ đạo không hoàn toàn tròn, nhưng có thể coi gần đúng là chuyển động tròn.
-
Các thiết bị quay: Ví dụ như động cơ, quạt, bánh xe…
-
Trong công nghiệp: Chuyển động của băng tải, các chi tiết máy quay…
V. Bài Tập Vận Dụng
Ví dụ 1: Một chiếc xe đạp di chuyển trên đường tròn có bán kính 10m với tốc độ không đổi 5m/s. Tính tốc độ góc và gia tốc hướng tâm của xe.
Giải:
- Tốc độ góc: (omega = frac{v}{r} = frac{5}{10} = 0.5 (rad/s))
- Gia tốc hướng tâm: ( a_{ht}=dfrac{v^{^{2}}}{r}=dfrac{5^2}{10} = 2.5 (m/s^2))
Ví dụ 2: Một cánh quạt quay với tần số 1200 vòng/phút. Tính chu kỳ và tốc độ góc của cánh quạt.
Giải:
- Đổi tần số: f = 1200 vòng/phút = 20 vòng/giây = 20 Hz
- Chu kỳ: (T = frac{1}{f} = frac{1}{20} = 0.05 (s))
- Tốc độ góc: (omega = 2pi f = 2pi .20 = 40pi (rad/s))
VI. Sơ Đồ Tư Duy Chuyển Động Tròn Đều
Alt: Sơ đồ tư duy chuyển động tròn đều, tóm tắt các khái niệm, công thức và mối liên hệ giữa các đại lượng như vận tốc dài, tốc độ góc, chu kỳ, tần số và gia tốc hướng tâm.
Sơ đồ tư duy này giúp hệ thống hóa kiến thức về chuyển động tròn đều một cách trực quan và dễ nhớ.