Một bài toán điển hình về chuyển động đều thường gặp trong chương trình Toán lớp 9 là: Một ô Tô Dự định đi Từ A đến B trong một khoảng thời gian nhất định. Bài toán này thường xoay quanh việc tính toán vận tốc, thời gian và quãng đường, đồng thời liên hệ chúng với các điều kiện thay đổi để tìm ra đáp số.
Để giải quyết các bài toán dạng này, chúng ta thường sử dụng phương pháp lập hệ phương trình. Các yếu tố cần quan tâm bao gồm:
- Vận tốc dự định: Vận tốc mà ô tô dự định đi.
- Thời gian dự định: Thời gian mà ô tô dự định đi hết quãng đường.
- Quãng đường AB: Độ dài quãng đường mà ô tô cần đi.
Khi vận tốc thay đổi (tăng hoặc giảm), thời gian di chuyển cũng sẽ thay đổi theo, và từ đó chúng ta có thể thiết lập các phương trình liên quan.
Ví dụ, một bài toán điển hình như sau:
Một ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 3 giờ, còn nếu xe chạy chậm lại mỗi giờ 10km thì đến nơi chậm mất 5 giờ. Tính vận tốc của xe lúc ban đầu.
Lời giải chi tiết cho bài toán này như sau:
Gọi vận tốc ban đầu của ô tô là x (km/h) và thời gian dự định đi là y (giờ). Điều kiện là x > 10.
Quãng đường AB có thể được tính bằng công thức: S = x.y
Khi xe chạy nhanh hơn 10km/h, vận tốc mới là x + 10 (km/h) và thời gian đi là y – 3 (giờ). Quãng đường vẫn là AB, nên ta có phương trình:
(x + 10)(y – 3) = x.y
Khi xe chạy chậm hơn 10km/h, vận tốc mới là x – 10 (km/h) và thời gian đi là y + 5 (giờ). Quãng đường vẫn là AB, nên ta có phương trình:
(x – 10)(y + 5) = x.y
Từ đó, ta có hệ phương trình:
(x + 10)(y - 3) = xy
(x - 10)(y + 5) = xyGiải hệ phương trình này, ta sẽ tìm được giá trị của x và y, từ đó xác định được vận tốc ban đầu của ô tô.
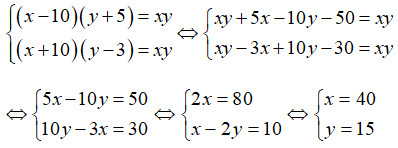Hệ phương trình toán học minh họa cách giải bài toán ô tô đi từ A đến B
Minh họa hệ phương trình dùng để giải bài toán về vận tốc và thời gian của một ô tô dự định đi từ A đến B.
Trong bài toán này, sau khi giải hệ phương trình, ta tìm được vận tốc ban đầu của ô tô là 40 km/h.
Các dạng bài tập mở rộng:
Ngoài dạng bài cơ bản trên, các bài toán về “một ô tô dự định đi từ A đến B” có thể được biến đổi theo nhiều hướng khác nhau, ví dụ:
- Bài toán có thể yêu cầu tính thời gian dự định, quãng đường AB, hoặc cả hai.
- Bài toán có thể đưa ra các điều kiện phức tạp hơn về sự thay đổi vận tốc và thời gian. Ví dụ, xe đi một phần quãng đường với vận tốc này, sau đó thay đổi vận tốc.
- Bài toán có thể kết hợp với các yếu tố khác như nghỉ giữa đường, hoặc sự cố kỹ thuật.
Để giải quyết các bài toán phức tạp hơn, việc quan trọng là phải phân tích kỹ đề bài, xác định rõ các yếu tố đã biết và chưa biết, và thiết lập các phương trình một cách chính xác. Sử dụng sơ đồ hoặc bảng biểu có thể giúp bạn hình dung rõ hơn mối quan hệ giữa các yếu tố và tìm ra hướng giải quyết phù hợp.
