Hình thoi là một hình tứ giác đặc biệt, quen thuộc trong cả toán học và đời sống. Bài viết này sẽ giúp bạn hiểu rõ về “Một Hình Thoi Có độ Dài”, từ định nghĩa, công thức tính diện tích, các dạng bài tập thường gặp đến những ứng dụng thực tế thú vị.
Giới Thiệu Về Hình Thoi
Hình thoi là một tứ giác có bốn cạnh bằng nhau. Nó có nhiều ứng dụng trong kiến trúc, thiết kế và tự nhiên.
.jpg)
Alt: Định nghĩa hình thoi và dấu hiệu nhận biết chính xác: bốn cạnh bằng nhau, hai đường chéo vuông góc.
Để nhận biết một hình thoi, bạn cần nhớ những đặc điểm sau:
- Bốn cạnh có độ dài bằng nhau.
- Hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.
- Các góc đối diện bằng nhau.
Công Thức Tính Diện Tích Hình Thoi Khi Biết Độ Dài
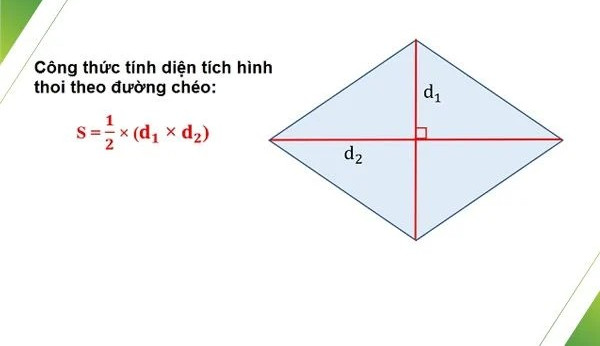
Công thức cơ bản nhất để tính diện tích hình thoi dựa vào độ dài hai đường chéo là:
S = (d1 × d2) / 2
Trong đó:
- S là diện tích hình thoi.
- d1 và d2 là độ dài hai đường chéo.
Ví dụ: Một hình thoi có đường chéo d1 = 6cm và d2 = 8cm. Diện tích hình thoi là S = (6 × 8) / 2 = 24 cm².
Alt: Minh họa công thức tính diện tích hình thoi S = (d1 x d2)/2, với d1 và d2 là độ dài hai đường chéo.
Các Dạng Toán Liên Quan Đến Độ Dài Của Hình Thoi
Có nhiều dạng bài tập liên quan đến việc tính diện tích hình thoi, trong đó, độ dài đóng vai trò quan trọng. Dưới đây là một số dạng thường gặp:
Dạng 1: Tính Diện Tích Khi Biết Độ Dài Hai Đường Chéo
Đây là dạng bài tập cơ bản nhất. Bạn chỉ cần áp dụng trực tiếp công thức S = (d1 × d2) / 2.
Ví dụ: Tính diện tích hình thoi khi biết độ dài hai đường chéo lần lượt là 10cm và 14cm.
Dạng 2: Tính Diện Tích Khi Biết Độ Dài Cạnh Và Chiều Cao
Trong trường hợp này, diện tích hình thoi được tính bằng công thức:
S = a × h
Trong đó:
- a là độ dài cạnh hình thoi.
- h là chiều cao hình thoi (khoảng cách giữa hai cạnh đối diện).
Alt: Hình ảnh minh họa công thức tính diện tích hình thoi khi biết chiều cao h và cạnh đáy a.
Dạng 3: Tính Diện Tích Khi Biết Độ Dài Cạnh Và Một Góc
Khi biết độ dài cạnh và một góc của hình thoi, ta có thể sử dụng công thức lượng giác:
S = a² × sin(α)
Trong đó:
- a là độ dài cạnh hình thoi.
- α là một trong các góc của hình thoi.
Ví dụ: Cho hình thoi có cạnh dài 5cm và một góc bằng 60 độ. Tính diện tích hình thoi.
Alt: Hình vẽ minh họa công thức diện tích hình thoi S = a^2 sin(alpha) với a là độ dài cạnh và alpha là góc.*
Lưu Ý Quan Trọng Khi Giải Bài Tập Về Hình Thoi
Khi giải các bài toán liên quan đến diện tích hình thoi, cần chú ý những điểm sau:
- Đọc kỹ đề bài: Xác định rõ các yếu tố đã cho (độ dài đường chéo, cạnh, góc, chiều cao) và yêu cầu của bài toán.
- Đơn vị đo: Kiểm tra xem tất cả các đại lượng đã cho có cùng đơn vị đo hay không. Nếu không, cần quy đổi về cùng một đơn vị trước khi thực hiện tính toán.
- Vẽ hình: Vẽ hình minh họa giúp hình dung bài toán và tránh nhầm lẫn.
Alt: Biểu tượng lưu ý, nhấn mạnh sự cẩn trọng khi giải các bài toán liên quan đến hình thoi.
Ứng Dụng Thực Tế Của Việc Tính Diện Tích Hình Thoi
Việc tính diện tích hình thoi không chỉ có ý nghĩa trong học tập mà còn có nhiều ứng dụng trong thực tế, cụ thể như:
- Xây dựng và kiến trúc: Tính toán vật liệu cần thiết khi ốp lát gạch hình thoi, thiết kế mái nhà, v.v.
- Thiết kế thời trang: Tính toán lượng vải cần thiết để tạo ra các họa tiết hình thoi trên trang phục.
- Nông nghiệp: Tính diện tích các khu đất canh tác có hình thoi.
- Thiết kế đồ họa: Sử dụng trong thiết kế logo, banner quảng cáo có hình thoi.
Alt: Hình ảnh về các vật dụng và kiến trúc trong đời sống có hình dạng hình thoi.
Bài Tập Thực Hành Về Độ Dài Và Diện Tích Hình Thoi
Dưới đây là một số bài tập để bạn luyện tập:
- Tính diện tích hình thoi có độ dài hai đường chéo là 8cm và 12cm.
- Một hình thoi có diện tích 24cm² và một đường chéo dài 6cm. Tính độ dài đường chéo còn lại.
- Tính diện tích hình thoi có cạnh dài 5cm và chiều cao 4cm.
- Một hình thoi có cạnh dài 7cm và một góc 30°. Tính diện tích hình thoi.
Alt: Ảnh minh họa bài tập về hình thoi dành cho học sinh lớp 4, tập trung vào tính diện tích.
Kết Luận
Hiểu rõ về “một hình thoi có độ dài” và cách tính diện tích của nó giúp chúng ta ứng dụng kiến thức vào giải quyết nhiều vấn đề thực tế. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn tự tin hơn khi đối mặt với các bài toán hình học. Hãy luyện tập thường xuyên để nắm vững kiến thức nhé!