Trong toán học và cuộc sống, hình chữ nhật là một hình học phổ biến. Việc nắm vững các khái niệm liên quan đến hình chữ nhật, đặc biệt là “nửa chu vi”, giúp chúng ta giải quyết nhiều bài toán và ứng dụng thực tế.
Nửa chu vi của hình chữ nhật là gì?
Nửa chu vi của một hình chữ nhật là tổng độ dài của chiều dài và chiều rộng của hình đó. Nếu gọi chiều dài là a và chiều rộng là b, thì nửa chu vi sẽ là: a + b.
Bài toán ví dụ về nửa chu vi hình chữ nhật
Bài toán 25: Một thửa ruộng hình chữ nhật có nửa chu vi là 75 m và chiều rộng là 25 m.
a) Tính diện tích của thửa ruộng.
b) Người ta trồng ngô trên thửa ruộng đó, tính ra trung bình 1 m2 đất thu được $frac{1}{2}$ kg ngô. Hỏi cả thửa ruộng thu được bao nhiêu ki-lô-gam ngô?
Để giải bài toán này, ta cần tìm chiều dài của thửa ruộng, sau đó tính diện tích và lượng ngô thu hoạch được.
Giải:
a) Chiều dài thửa ruộng là: 75 m – 25 m = 50 m
Diện tích thửa ruộng là: 50 m * 25 m = 1250 m2
b) Số ki-lô-gam ngô thu được là: 1250 m2 * $frac{1}{2}$ kg/m2 = 625 kg
Ứng dụng của nửa chu vi trong thực tế
Nửa chu vi không chỉ là một khái niệm toán học mà còn có nhiều ứng dụng thực tế. Ví dụ, khi bạn muốn rào một khu vườn hình chữ nhật và biết tổng số mét rào có thể sử dụng (tức là chu vi), bạn có thể chia đôi số mét đó để biết nửa chu vi. Điều này giúp bạn xác định chiều dài và chiều rộng phù hợp cho khu vườn của mình.
Các bài toán liên quan đến diện tích và chu vi
Nhiều bài toán liên quan đến hình chữ nhật kết hợp cả diện tích và chu vi (hoặc nửa chu vi). Việc hiểu rõ mối quan hệ giữa các yếu tố này giúp chúng ta giải quyết các bài toán một cách hiệu quả.
Bài toán về lựa chọn vị trí dựng trại
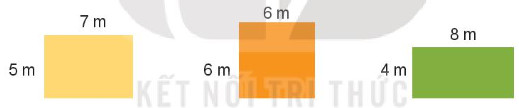
Bài toán 2: Các bạn khối lớp Bốn đang chuẩn bị cho buổi Hội trại mùa Thu của trường. Lớp em được chọn một trong ba vị trí để dựng trại có kích thước như hình dưới đây. Em chọn vị trí nào để có diện tích lớn nhất?
Bài toán lựa chọn vị trí dựng trại dựa trên diện tích. Cần so sánh diện tích các hình chữ nhật để đưa ra quyết định tốt nhất. “Vi tri dung trai dien tich lon nhat”
Để giải quyết bài toán này, chúng ta cần tính diện tích của từng vị trí và so sánh chúng.
Bài toán về tính diện tích cần sơn
Bài toán 16: Người ta sơn một bức tường có dạng hình chữ nhật với kích thước như hình vẽ dưới đây. Hãy tính diện tích cần sơn, biết rằng tổng diện tích cửa sổ và cửa ra vào là 6 m2.
Bài toán tính diện tích cần sơn, cần tính diện tích hình chữ nhật và trừ đi phần diện tích không sơn (cửa sổ và cửa ra vào). “dien tich can son buc tuong hinh chu nhat”
Để giải bài toán này, chúng ta cần tính diện tích tổng của bức tường hình chữ nhật, sau đó trừ đi diện tích của cửa sổ và cửa ra vào.
Bài toán về lát gạch nền nhà
Bài toán 12: Người ta dùng loại gạch men hình vuông có cạnh 50 cm để lát nền một phòng học hình chữ nhật có chiều dài 8 m, chiều rộng 6 m. Hỏi cần bao nhiêu viên gạch men loại đó để vừa đủ lát kín nền phòng học? (Diện tích phần mạch vữa không đáng kể.)
Để giải bài toán này, chúng ta cần tính diện tích của nền phòng học và diện tích của một viên gạch, sau đó chia diện tích nền phòng học cho diện tích một viên gạch để tìm số lượng gạch cần thiết.
Kết luận
Hiểu rõ về “Một Hình Chữ Nhật Có Nửa Chu Vi” và các khái niệm liên quan đến diện tích, chu vi giúp chúng ta giải quyết nhiều bài toán thực tế. Việc luyện tập thường xuyên và áp dụng kiến thức vào các tình huống cụ thể sẽ giúp bạn nắm vững kiến thức và phát triển tư duy toán học.